Загрузка...
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора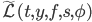 
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы 
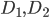. Это матрицы размерностью 
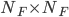, где, для 
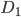(согласно определению в части 4) в ячейках [j,j] стоят -1, если 
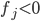и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если 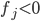и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если 
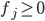и 0 - в остальных случаях. Как составить матрицу 
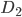, я думаю, вы догадаетесь сами, взглянув на ее определение в части 4 цикла статей.
Далее, определение для матожидания квадратичного и линейного изменения цены:
![\mathbb{E}_td[P,P]_t=(\frac{1}{4}\lambda^J_1+\lambda^J_2)dt](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_f31079b3033c3cd9d3e4e5aa65d00c6e.gif)
, где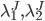 
- интенсивность скачков цены на полшага и один шаг соответственно.
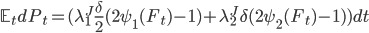, где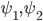 
- вероятности скачков цены - см. часть 2.
Оператор воздействия величины спреда на функцию владения:
![\mathcal{L}^S\circ v(t,y,f,s)=\Bigg(\sum\limits_{j=1}^3 \rho_{ij}[v(t,y,f,j\delta)-v(t,y,f,i\delta)]\Bigg)\lambda^S](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_80b84f646b665acb4947185588a4a2c5.gif)
, где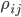 
- элементы матрицы переходов марковского процесса скачков спреда, 
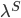- интенсивность этих скачков.
В выше приведенных формулах все интенсивности могут быть получены из рыночных данных путем простого расчета, например, можно подсчитать количество скачков спреда за определенный промежуток времени и параметр 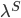будет равен этому количеству, деленному на длительность промежутка в секундах. Интенсивности 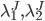считаются аналогичным образом для скачков средней цены стакана на полшага и один шаг соответственно. Матрицу переходов тоже легко получить, подсчитав, сколько раз спред переходил из состояния один шаг цены в состояние два шага цены, из состояния один шаг цены в состояние 3 шага цены, и т.д., заполнив элементы матрицы 
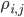, где i означает начальное состояние спреда, j - конечное состояние спреда, на главной диагонали 
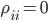. Приравняв сумму элементов в одной строке к 1, получим значения 
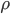, как доли от общей суммы ( элементы матрицы означают вероятности переходов).
Вероятности скачков цены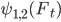 
тоже найти несложно. Для этого нужно подсчитать количество скачков средней цены на полшага (для 
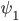), попадающее в диапазон значений дисбаланса в каждом из интервалов ![[f_j,f_{j+1}]](http://www.quantalgos.ru/wp-content/plugins/latex/cache/tex_94441f3d21b2994316acbacaba96d57d.gif)
, в каком-то промежутке времени, например, за один день, затем разделить величину в каждом интервале на общее число скачков. В результате получим плотность вероятности, интегрируя которую (складывая нарастающим итогом в численном варианте) в диапазоне всех значений дисбаланса f, получим исходные данные для нахождения формулы вероятности 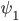. Далее методом наименьших квадратов, используя эти данные, находим коэффициент 
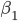аппроксимирующей функции 
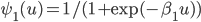. Все то же самое проделываем для функции 
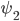, только скачки цены берем на полный шаг. Таким же образом получаем формулы для вероятностей взятия лимитных ордеров в очереди заявок h(f) (см. часть 3), только подсчитывать будем количество исполненных ордеров (для бида и аска отдельно) в каждом интервале дисбаланса f.
Нам осталось определить значения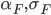 
из уравнения Орнштейна-Уленбека для процесса дисбаланса объемов 
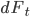(см.часть 2). Эти параметры находятся методом максимального правдоподобия, максимизируем следующую функцию:
где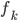 
- значение дисбаланса объема в момент времени 
,
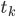, n - общее число значений k.
Итак, мы можем уже написать код для численного решения методом индукции. Ниже дан листинг на C#:
/* Функция решения уравнения HJB-QVI методом обратной индукции
* plt - структура, в которой определены основные переменные и политики
* plt.T - число временных точек расчета, plt.S - число значений спреда (=3)
* plt.F- число точек расчета дисбаланса объема, plt.Y - количество значений открытой позиции
* plt.dF - шаг величины дисбаланса объемов, plt.Fmax - модуль максимального значения дисбаланса
* plt.ticksize - минимальный шаг цены, plt.comiss - биржевая комиссия
* plt.w - массив значения численной функции владения
* plt.polmk - булевый массив, определяющий, какая политика будет использована при текущих значениях [t,y,f,s]
* если true - лимитные ордера, false - маркет ордера
* plt.thtkq - массив объемов маркет ордеров при действии политики маркет ордеров
* plt.thmka, plt.thmkb - массив значений 0 (выставление на лучшую цену) или 1 (выставление на шаг лучше лучшей цены)
* при действии политики лимитных ордеров
* maxlot - абсолютное максимальное значение открытой позиции
*/
public static void BackwardInduction(politics plt, int maxlot)
{
//Двигаемся вниз по временной сетке
for (int t = plt.T; t >= 0; t--)
{
//Двигаемся по сетке значения спреда
for (int s = 0; s < plt.S; s++)
{
// Определяем массив векторов оператора L (массив- по всем значениям открытой позиции,
//вектор оператора - по всем значениям дисбаланса)
double[][] L = new double[plt.Y][];
//Двигаемся по сетке открытых значений
for (int y = 0; y < plt.Y; y++)
{
// Инициализируем значения всех векторов L
L[y] = new double[plt.F];
//Вычисляем реальное значение открытой позиции из индекса
int yr = (int)(y - (plt.Y - 1) / 2);
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Реальное значение дисбаланса из индекса
double fr = plt.dF * f - plt.Fmax; ;
//Первый шаг - вычисление функции владения w в конечный момент времени T
if (t == plt.T) plt.w[y, f, s] = -Math.Abs(yr) * ((s + 1) * plt.ticksize / 2 + plt.commis);
else
{
//В остальные моменты времени находим значения векторов L (пока без умножения на
// дифференциальные матрицы в первой части выражения для L)
L[y][f] = LV(y, yr, fr, f, s, t, plt);
}
}
if (t < plt.T)
{
//Перемножение матричной части и векторов L, полученных выше, в результате получаем
// полностью рассчитанные вектора L. plt.rmatrix - матричная часть
matrixmlt(plt.rmatrix, ref L[y]);
}
}
//Вычисление выражения M*L для определения политики маркет ордеров
if (t < plt.T)
{
//Двигаемся по сетке открытой позиции
for (int y = 0; y < plt.Y; y++)
{
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Максимальное значение контрактов, допустимое в маркет ордере на данном шаге
int dzmax = Math.Min(plt.Y - 1 - y, maxlot);
double ML = -1000000;
//Двигаемся по сетке объема маркет ордера
for (int dz = Math.Max(-y, -maxlot); dz <= dzmax; dz++)
{
//Вычисление оператора M*L для каждого значения объема маркет ордера
if (L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis) > ML)
{
ML = L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis);
//Занесение в политику маркет ордеров значения объема
plt.thtkq[t, y, f, s] = dz;
}
}
//Если оператор M*L больше оператора L при всех исходных параметрах, выбирается политика
//маркет ордеров
if (ML > L[y][f])
{
//Значению функции владения w присваивается значение оператора M*L
plt.w[y, f, s] = ML;
plt.polmk[t, y, f, s] = false;
}
// Иначе - политика лимитных ордеров
else
{
//Значению функции владения присваивается значение оператора L
plt.w[y, f, s] = L[y][f];
plt.polmk[t, y, f, s] = true;
}
}
}
}
}
}
}
//Функция вычисления значения оператора L, без перемножения на матричную часть
public static double LV(int y, int yr, double ft, int f, int s, int t, politics plt)
{
//Вычисление значений функции вероятности скачков цены на полшага и шаг psi1,2, с коэффициентами beta1,2
double psi1res = 0;
ClassMain.psifunc(plt.beta1, new double[] { ft }, ref psi1res, null);
double psi2res = 0;
ClassMain.psifunc(plt.beta2, new double[] { ft }, ref psi2res, null);
//Вычисление матожидания изменения средней цены, plt.lj1,plt.lj2 - интенсивности скачков цены
double Edp = plt.lj1 * (plt.ticksize / 2) * (2 * psi1res - 1) + plt.lj2 * plt.ticksize * (2 * psi2res - 1);
//Вычисление оператора воздействия спреда на функцию владения, plt.ro - матрица переходов состояний спреда
double Ls = 0;
for (int j = 0; j < plt.ro.GetLength(1); j++)
{
Ls += (plt.w[y, f, j] - plt.w[y, f, s]) * plt.ro[s, j];
}
//plt.ls - интенсивность скачков спреда
Ls = plt.ls * Ls;
//Вычисление матожидания среднеквадратичного изменения цены
double Edpp = (0.25 * plt.lj1 + plt.lj2);
double gv = -10000000;
int thmax = 1;
if (s == 0) thmax = 0;
double gvtemp = 0;
//Вычисление значений вероятности взятия лимитных ордеров в очереди заявок h(f)
//plt.ch - коэффициент в формуле для вероятности h(f)
double hresp = 0;
ClassMain.htfunc(plt.ch, new double[] { ft }, ref hresp, null);
double hresm = 0;
ClassMain.htfunc(plt.ch, new double[] { -ft }, ref hresm, null);
//Вычисление слагаемых ga и gb в выражении для оператора L, thmax - максимальное значение, которое принимает
// политика для лимитных ордеров - 1
for (int i = 0; i <= thmax; i++)
{
for (int k = 0; k <= thmax; k++)
{
gvtemp = (i * (plt.lMa) + (1 - i) * plt.lMa * hresp) * (plt.w[Math.Min(y + 1, (int)(2 * plt.Ymax)), f, s] - plt.w[y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * i) +
(k * (plt.lMb) + (1 - k) * plt.lMb * hresm) * (plt.w[Math.Max(y - 1, 0), f, s] - plt.w[y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if (gvtemp > gv)
{
gv = gvtemp;
plt.thmkb[t, y, f, s] = i; plt.thmka[t, y, f, s] = k;
}
}
}
//Вычисление значения оператора L (без умножения на матричную часть)
//plt.dt- шаг времени, plt.gamma - мера риска
double lv = plt.w[y, f, s] + plt.dt * yr * Edp + plt.dt * Ls - plt.dt * plt.gamma * yr * yr * Edpp + plt.dt * gv;
return lv;
}
И приведу отдельный листинг вычисления матричной части выражения для оператора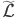 
:
//Вычисление матричной части выражения оператора L
public void MatrixSolve()
{
//Дифференциальные матрицы D1,2 и матрица идентичности I.
double[,] D1 = new double[F, F];
double[,] D2 = new double[F, F];
double[,] I = new double[F, F];
//Заполняем матрицы на сетке F x F
for (int i = 0; i < F; i++)
{
int k = 0;
if (i <= (F - 1) / 2) k = i;
else k = i - 1;
D1[i, k] = -1 / dF; D1[i, k + 1] = 1 / dF;
if (i == 0)
{
D2[i, i + 1] = 2 / (dF * dF);
}
else if (i == F - 1)
{
D2[i, i - 1] = 2 / (dF * dF);
}
else
{
D2[i, i - 1] = 1 / (dF * dF);
D2[i, i + 1] = 1 / (dF * dF);
}
D2[i, i] = -2 / (dF * dF);
I[i, i] = 1;
double Ft = dF * i - Fmax;
//Вычисляем значения матричной части выражения оператора L
//cft[1] - значение sigmaF из уравнения Орнштейна-Уленбека для Ft,
//cft[0] - значение alfaF
for (int j = 0; j < F; j++)
{
rmatrix[i, j] = I[i, j] - 0.5*dt * cft[1] * cft[1] * D2[i, j] - dt * cft[0] * Ft * D1[i, j];
}
}
alglib.matinvreport rep;
int info;
//Инвертируем матрицу, используя стороннюю библиотеку alglib
alglib.rmatrixinverse(ref rmatrix, out info, out rep);
}
На этом цикл статей по алгоритмам маркет мейкера завершен. Можно ли применить рассмотренную стратегию в реальной торговле? Несомненно, да. Но использование дисбаланса объемов F как сигнала предсказания цены, возможно, не будет достаточно эффективно, так как этот сигнал работает на очень коротком промежутке времени. Но нам ничего не мешает несколько модифицировать его, сохранив у нового сигнала следование процессу Орнштейна-Уленбека, что не изменит нахождение его параметров. И в таком случае получим полноценный HFT алгоритм со всеми его преимуществами.
Буду рад вашим отзывам по данным статьям и указаниям на ошибки, если таковые присутствуют в тексте.
P.S. Ниже публикую код, предоставленный пользователем Eskalibur. В нем исправлены некоторые ошибки, найденные в моем коде, и достигнуто полное соответствие математической модели, представленной в оригинальной статье. Eskaliburу за это огромное спасибо.
/* Функция решения уравнения HJB-QVI методом обратной индукции
* plt - структура, в которой определены основные переменные и политики
* plt.T - число временных точек расчета, plt.S - число значений спреда (=3)
* plt.F- число точек расчета дисбаланса объема, plt.Y - количество значений открытой позиции
* plt.dF - шаг величины дисбаланса объемов, plt.Fmax - модуль максимального значения дисбаланса
* plt.ticksize - минимальный шаг цены, plt.comiss - биржевая комиссия
* plt.w - массив значения численной функции владения
* plt.polmk - булевый массив, определяющий, какая политика будет использована при текущих значениях [t,y,f,s]
* если true - лимитные ордера, false - маркет ордера
* plt.thtkq - массив объемов маркет ордеров при действии политики маркет ордеров
* plt.thmka, plt.thmkb - массив значений 0 (выставление на лучшую цену) или 1 (выставление на шаг лучше лучшей цены)
* при действии политики лимитных ордеров
* maxlot - абсолютное максимальное значение открытой позиции
*/
public static void BackwardInduction(politics plt, int maxlot)
{
double[][] L = new double[plt.Y][];
for (int y = 0; y < plt.Y; y++)L[y] = new double[plt.F];
//Двигаемся вниз по временной сетке
for (int t = plt.T; t >= 0; t--)
{
//Двигаемся по сетке значения спреда
for (int s = 0; s < plt.S; s++)
{
// Определяем массив векторов оператора L (массив- по всем значениям открытой позиции,
//вектор оператора - по всем значениям дисбаланса)
//Двигаемся по сетке открытых значений
for (int y = 0; y < plt.Y; y++)
{
//Вычисляем реальное значение открытой позиции из индекса
int yr = (int)(y - (plt.Y - 1) / 2);
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Реальное значение дисбаланса из индекса
double fr = plt.dF * f - plt.Fmax;
//Первый шаг - вычисление функции владения w в конечный момент времени T
if (t == plt.T) plt.w[t, y, f, s] = -Math.Abs(yr) * ((s + 1) * plt.ticksize / 2 + plt.commis);
else
{
//В остальные моменты времени находим значения векторов L (пока без умножения на
// дифференциальные матрицы в первой части выражения для L)
L[y][f] = LV(y, yr, fr, f, s, t, plt);
}
}
if (t < plt.T)
{
//Перемножение матричной части и векторов L, полученных выше, в результате получаем
// полностью рассчитанные вектора L. plt.rmatrix - матричная часть
matrixmlt(plt.rmatrix, ref L[y]);
}
}
//Вычисление выражения M*L для определения политики маркет ордеров
if (t < plt.T)
{
//Двигаемся по сетке открытой позиции
for (int y = 0; y < plt.Y; y++)
{
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Максимальное значение контрактов, допустимое в маркет ордере на данном шаге
int dzmax = Math.Min(plt.Y - 1 - y, maxlot);
double ML = -1000000;
//Двигаемся по сетке объема маркет ордера
for (int dz = Math.Max(-y, -maxlot); dz <= dzmax; dz++)
{
//Вычисление оператора M*L для каждого значения объема маркет ордера
if (L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis) > ML)
{
ML = L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis);
//Занесение в политику маркет ордеров значения объема
plt.thtkq[t, y, f, s] = dz;
}
}
//Если оператор M*L больше оператора L при всех исходных параметрах, выбирается политика
//маркет ордеров
if (ML > L[y][f])
{
//Значению функции владения w присваивается значение оператора M*L
plt.w[t, y, f, s] = ML;
plt.polmk[t, y, f, s] = false;
}
// Иначе - политика лимитных ордеров
else
{
//Значению функции владения присваивается значение оператора L
plt.w[t, y, f, s] = L[y][f];
plt.polmk[t, y, f, s] = true;
}
}
}
}
}
}
delete[][] L;
}
//Функция вычисления значения оператора L, без перемножения на матричную часть
public static double LV(int y, int yr, double ft, int f, int s, int t, politics plt)
{
//Вычисление значений функции вероятности скачков цены на полшага и шаг psi1,2, с коэффициентами beta1,2
double psi1res = 0;
ClassMain.psifunc(plt.beta1, new double[] { ft }, ref psi1res, null);
double psi2res = 0;
ClassMain.psifunc(plt.beta2, new double[] { ft }, ref psi2res, null);
//Вычисление матожидания изменения средней цены, plt.lj1,plt.lj2 - интенсивности скачков цены
double Edp = plt.lj1 * (plt.ticksize / 2) * (2 * psi1res - 1) + plt.lj2 * plt.ticksize * (2 * psi2res - 1);
//Вычисление оператора воздействия спреда на функцию владения, plt.ro - матрица переходов состояний спреда
double Ls = 0;
for (int j = 0; j < plt.ro.GetLength(1); j++)
{
Ls += (plt.w[t+1, y, f, j] - plt.w[t+1, y, f, s]) * plt.ro[s, j];
}
//plt.ls - интенсивность скачков спреда
Ls = plt.ls * Ls;
//Вычисление матожидания среднеквадратичного изменения цены
double Edpp = (0.25 * plt.lj1 + plt.lj2);
double gv = -10000000;
int thmax = 1;
if (s == 0) thmax = 0;
double gvtemp = 0;
//Вычисление значений вероятности взятия лимитных ордеров в очереди заявок h(f)
//plt.ch - коэффициент в формуле для вероятности h(f)
double hresp = 0; //вероятность аск
ClassMain.htfunc(plt.ch, new double[] { ft }, ref hresp, null);
double hresm = 0; //вероятность бидов
ClassMain.htfunc(plt.ch, new double[] { -ft }, ref hresm, null);
//Вычисление слагаемых ga и gb в выражении для оператора L, thmax - максимальное значение, которое принимает
// политика для лимитных ордеров - 1
for (int i = 0; i <= thmax; i++)
{
for (int k = 0; k <= thmax; k++)
{
gvtemp = (i * (plt.lMa) + (1 - i) * plt.lMa * hresp) * (plt.w[t+1, Math.Min(y + 1, (int)(2 * plt.Ymax)), f, s] - plt.w[t+1, y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * i) +
(k * (plt.lMb) + (1 - k) * plt.lMb * hresm) * (plt.w[t+1, Math.Max(y - 1, 0), f, s] - plt.w[t+1, y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if (gvtemp > gv)
{
gv = gvtemp;
plt.thmkb[t, y, f, s] = i; plt.thmka[t, y, f, s] = k;
}
}
}
//Вычисление значения оператора L (без умножения на матричную часть)
//plt.dt- шаг времени, plt.gamma - мера риска
double lv = plt.w[t+1, y, f, s] + plt.dt * yr * Edp + plt.dt * Ls - plt.dt * plt.gamma * yr * yr * Edpp + plt.dt * gv;
return lv;
}
//
//Вычисление матричной части выражения оператора L
public void MatrixSolve()
{
//Дифференциальные матрицы D1,2 и матрица идентичности I.
int j;
double[,] D1 = new double[F, F];
double[,] D2 = new double[F, F];
double[,] I = new double[F, F];
//Заполняем матрицы на сетке F x F
for (int i = 0; i < F; i++)
{
for (int j = 0; j < F; j++){ //обязательно необходимо приводить начальные значения.
D1[i][j]=0; //может получиться так, что вместо 0 в элементе массива будет число
D2[i][j]=0; // =1e-312, и эту ошибку потом очень непросто обнаружить, "эффект бабочки"
if(i==j)I[i][j]=1;
else I[i][j]=0;
};
//
int k = 0;
if (i <= (F - 1) / 2) k = i;
else k = i - 1;
D1[i, k] = -1 / dF; D1[i, k + 1] = 1 / dF;
if (i == 0)
{
D2[i, i + 1] = 1 / (dF * dF);
D2[i, i] = -2 / (dF * dF);
}
else if (i == F - 1)
{
D2[i, i - 1] = 1 / (dF * dF);
D2[i, i] = -2 / (dF * dF);
}
else
{
D2[i, i - 1] = 1 / (dF * dF);
D2[i, i + 1] = 1 / (dF * dF);
D2[i, i] = -2 / (dF * dF);
}
double Ft = dF * i - Fmax;
//Вычисляем значения матричной части выражения оператора L
//cft[1] - значение sigmaF из уравнения Орнштейна-Уленбека для Ft,
//cft[0] - значение alfaF
for (j = 0; j < F; j++)
{
rmatrix[i, j] = I[i, j] - 0.5*dt * cft[1] * cft[1] * D2[i, j] - dt * cft[0] * Ft * D1[i, j];
}
}
alglib.matinvreport rep;
int info;
//Инвертируем матрицу, используя стороннюю библиотеку alglib
alglib.rmatrixinverse(ref rmatrix, out info, out rep);
delete[,] D1;
delete[,] D2;
delete[,] I;
}
Скажите, этот алгоритм реально работает? И в чем преимущество данного метода перед эмпирическим подходом - когда дисбаланс объема можно отследить из истории и использовать полученные значения для оценки вероятности смещения цены?
Алгоритм применим к реальной торговле. Как вы его допилите, в каком виде в итоге он дойдет до торгов - это уже ваша работа, путем тестирования и затем испытания в реале. Эмпирический подход он и есть эмпирический, то есть не оптимальный. Высокочастотную систему на таком подходе не построишь, максимум что-нибудь с сомнительными статистическими характеристиками
Я вас понял, просто за математикой часто не видно практической пользы, а простые вещи зачастую слишком усложняются.
Ведь, например, в цикле ваших статей вы используете ряд моделей (Орштейн-Уленбек для объемов в стакане, Jump-процесс для моделирования движения цены и т.д.), как вы объясните, что именно эти модели являются оптимальными, а не какие-то другие? Где говорится о преимуществах и недостатках этих моделей?
Зачем вообще нужны модели, когда в конечном счете цена вероятней сдвинется вверх когда на бьест аске заявок мало, а на бест биде - много. практику остается только собрать данные, провести большую работу по анализу данных и получить в итоге тоже самое, что дает модельный подход?
Я ни в коем случае не умиляю целесообразности модельного подхода, просто в чем именно заключается его преимущество?
Кстати, что посоветуете прочитать именно по математике для понимания того, что вы пишите, а то уж как-то тяжело идет, плюс совсем не понятно как эту математику на код перекладывать?
Общий недостаток сбора и эмпирического анализа данных в том, что, как правило, получается подгонка под исторические данные. Такие системы если и будут работать, то непродолжительное время - я в курсе про тестирование на разделенных выборках и т.п., но это не помогает в большинстве случаев. Если же в основе лежит мат. модель - и есть понимание, откуда взялись ее параметры, то вы всегда сможете быстро скорректировать свои алгоритмы, если вдруг их прибыльность стала падать, ведь процесс, с которого вы зарабатывали, не исчезнет в один момент, он будет всегда, просто его параметры изменяются в течение времени, а его работоспособность подтверждена статистической вероятностью. Что касается самих моделей, ну Орнештейн-Уленбек - это когда какой-то процесс вращается вокруг среднего значения с определенной волатильностью. Подходит ли под это определение дисбаланс объемов? На конечных промежутках времени несомненно, и этого уже достаточно для того, чтобы основные расчеты, основанные на этой модели, оказались верными. Посоветовать что-то определенное из книг по математике не могу, я читал по мере надобности из разных источников, хотя считаю, что для понимания данных статей достаточно школьного курса - просто надо разобраться, ничего сложного там нет.
Кстати, вот еще интересный подход:
http://www.columbia.edu/~ww2040/orderbook.pdf - моделируют всю глубину книги и маркеты / отмены лимиток пуассоновскими процессами с разной интенсивностью поступления заявок, интенсивности считают на основе средних по всем своим данным и опять-таки согласно эмпирической функции, что считаю неверным, т.к. интенсивности в реале тоже меняются во времени, как и величина средней заявки маркета/лимитника.
А дальше используют преобразование Лапласа для подсчета вероятности смещения цены в зависимости от кол-ва ордеров на бидах/асках.
Посмотрите если будет время, на ваш взгляд это целесообразный подход? (Заметьте опять-таки, эмпрические данные оценки вероятности у них не так уж сильно и разнятся с моделью)
Матрица переходов, разве не так Pij=(Qij)/Q, где Q - количество всех переходов, (подсчитываемых при подсчёте интенсивности переходов), а Qij - количество переходов из i в j ?
Все понятно... действительно достаточно приравнять к 1 сумму элементов одной строки. Это будет полное пространство вероятностей.
Итак, добавлю, параметры процесса Орнштейна-Уленбека помимо ММП можно оценивать и МНК, так как процесс удовлетворяет свойству Марковости. G - в таком случае вычисляется как остатки от регрессии.
Регрессия строится не по t, а по y(i-1)
Всё таки, пришлось разобраться глубоко. Алгоритм в текущем виде не рабочий. Мало того, он имеет несколько грубейших ошибок, в частности:
Ошибка 1. функция w[y,f,s] в алгоритме используется независимой от t. На самом деле на каждом шаге в алгоритме используется значение функции w[t+1,y,f,s], А в конце вычисления оператор больший из операторов L и М*L приравнивается значению w[t,y,f,s]. - который затем используется в следующей итерации. Замечу, что при правильном построении алгоритма вычисления становятся неусточивыми, и функция w стремиться +-inf. Это происходит потому, что неправильно оцениваются некоторые характеристики, а именно вероятности. После проверки правильного решения я поясню ниже, как же всё таки правильно оценивать эти немудрёные величины, в результате чего вязкое решение станет устойчивым, и даст верные и хорошие политики на выходе.
Оцениваются правильно. Но решение тем не менее не устойчиво. Неусточивость вносится вычислением оператора Ls, если интенсивность скачков спреда высока. Как разберусь в чем собственно дело, напишу.
неверно. Вычисление методом индукции происходит по времени с обратным отсчетом, поэтому функция w[y,f,s] в каждой итерации и является по сути w[t+1,y,f,s].
Спасибо за ответ, но Вы ошибаетесь. Вычисления происходят с обратным отсчётом по времени. В терминальный момент времени вычисляется значение w[t,y,f,s]. В следующей итерации в вычислениях используется значение w[t+1,y,f,s] - вычисленное на предыдущем шаге, и определяется новое значение w[t,y,f,s] для каждого y,f,s. Это метод обратной индукции и так он описан в статье JIANGMIN XU "Optimal Strategies of High Frequency Traders". В вашем случае, вычисленная при каждом значении y и f функции w[y,f,s] - изменяется для всякого s, и уже изменённая учавствует в вычислении в той же итерации по времени но для другого значения спреда - s. А так как все значения спреда связанны друг с другом через матрицы перехода в вычислениях накапливается ошибка. И в вашем алгоритме ошибка появляется и накапливается вот здесь:
double Ls = 0;
for (int j = 0; j < plt.ro.GetLength(1); j++)
{
Ls += (plt.w[y, f, j] - plt.w[y, f, s]) * plt.ro[s, j];
}
Если Вы не согласны пожалуйста проверьте.
В методе обратной индукции полученные новые значения функции владения w, учавствуют в вычислении только в следующей итерации. В вашем случае полученные значения уже влияют на новые значений функции при других значениях спреда в той же самой итерации. Так как мне не удалось (надеюсь временно) получить адекватные политики из-за неусточивости в решении, я не могу сказать точно где выражается ошибка в вашем алгоритме, но думаю что при значениях времени близких к Т, она проявляется в политиках при значении спреда 2 и 3, а при вермени близком к нулю, она должна по идее уже быть во всех значениях спреда, так как плавно расползается через матрицы перехода.
Итак, устойчивые решения получены. Ошибка определена.
снизу исправленный код.
/* Функция решения уравнения HJB-QVI методом обратной индукции
* plt - структура, в которой определены основные переменные и политики
* plt.T - число временных точек расчета, plt.S - число значений спреда (=3)
* plt.F- число точек расчета дисбаланса объема, plt.Y - количество значений открытой позиции
* plt.dF - шаг величины дисбаланса объемов, plt.Fmax - модуль максимального значения дисбаланса
* plt.ticksize - минимальный шаг цены, plt.comiss - биржевая комиссия
* plt.w - массив значения численной функции владения
* plt.polmk - булевый массив, определяющий, какая политика будет использована при текущих значениях [t,y,f,s]
* если true - лимитные ордера, false - маркет ордера
* plt.thtkq - массив объемов маркет ордеров при действии политики маркет ордеров
* plt.thmka, plt.thmkb - массив значений 0 (выставление на лучшую цену) или 1 (выставление на шаг лучше лучшей цены)
* при действии политики лимитных ордеров
* maxlot - абсолютное максимальное значение открытой позиции
*/
public static void BackwardInduction(politics plt, int maxlot)
{
//Двигаемся вниз по временной сетке
for (int t = plt.T; t >= 0; t--)
{
//Двигаемся по сетке значения спреда
for (int s = 0; s < plt.S; s++)
{
// Определяем массив векторов оператора L (массив- по всем значениям
//открытой позиции,
//вектор оператора - по всем значениям дисбаланса)
double[][] L = new double[plt.Y][]; //необходимо делать delete в конце
//цикла, иначе утечка памяти
//Двигаемся по сетке открытых значений
for (int y = 0; y < plt.Y; y++)
{
// Инициализируем значения всех векторов L
L[y] = new double[plt.F];
//Вычисляем реальное значение открытой позиции из индекса
int yr = (int)(y - (plt.Y - 1) / 2);
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Реальное значение дисбаланса из индекса
double fr = plt.dF * f - plt.Fmax; ;
//Первый шаг - вычисление функции владения w в
//конечный момент времени T
if(t==plt.T)plt.w[y,f,s]=-Math.Abs(yr)*((s+1)*plt.ticksize/2+plt.commis);
else
{ //В остальные моменты времени находим значения
//векторов L (пока без умножения на
//дифференциальные матрицы в первой части
//выражения для L)
L[y][f] = LV(y, yr, fr, f, s, t, plt);
}
}
if (t < plt.T)
{
//Перемножение матричной части и векторов L,
//полученных выше, в результате получаем
// полностью рассчитанные вектора L. plt.rmatrix -
//матричная часть
matrixmlt(plt.rmatrix, ref L[y]);
}
}
//Вычисление выражения M*L для определения политики маркет
//ордеров
}//завершение цикла для s
if (t < plt.T)
{
for(int s=0;s<plt.S;s++)
{
//Двигаемся по сетке открытой позиции
for (int y = 0; y < plt.Y; y++)
{
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Максимальное значение контрактов, допустимое
//в маркет ордере на данном шаге
int dzmax = Math.Min(plt.Y - 1 - y, maxlot);
double ML = -1000000;
//Двигаемся по сетке объема маркет ордера
for (int dz = Math.Max(-y, -maxlot); dz <= dzmax; dz++)
{
//Вычисление оператора M*L для каждого //
//значения объема маркет ордера
if (L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis) > ML)
{
ML = L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis);
//Занесение в политику маркет ордеров
//значения объема
plt.thtkq[t, y, f, s] = dz;
}
}
//Если оператор M*L больше оператора L при
//всех исходных параметрах, выбирается
//политика
//маркет ордеров
if (ML > L[y][f])
{
//Значению функции владения w
//присваивается значение оператора M*L
plt.w[t, y, f, s] = ML;
plt.polmk[t, y, f, s] = false;
}
// Иначе - политика лимитных ордеров
else
{
//Значению функции владения присваивается
//значение оператора L
plt.w[t, y, f, s] = L[y][f];
plt.polmk[t, y, f, s] = true;
}
}
}
}
}
}
}
//Функция вычисления значения оператора L, без перемножения на матричную часть
public static double LV(int y, int yr, double ft, int f, int s, int t, politics plt)
{
//Вычисление значений функции вероятности скачков цены на полшага и шаг psi1,2, с коэффициентами beta1,2
double psi1res = 0;
ClassMain.psifunc(plt.beta1, new double[] { ft }, ref psi1res, null);
double psi2res = 0;
ClassMain.psifunc(plt.beta2, new double[] { ft }, ref psi2res, null);
//Вычисление матожидания изменения средней цены, plt.lj1,plt.lj2 - интенсивности скачков цены
double Edp = plt.lj1 * (plt.ticksize / 2) * (2 * psi1res - 1) + plt.lj2 * plt.ticksize * (2 * psi2res - 1);
//Вычисление оператора воздействия спреда на функцию владения, plt.ro - матрица переходов состояний спреда
double Ls = 0;
for (int j = 0; j < plt.ro.GetLength(1); j++)
{
Ls += (plt.w[t+1,y, f, j] - plt.w[t+1,y, f, s]) * plt.ro[s, j];
}
//plt.ls - интенсивность скачков спреда
Ls = plt.ls * Ls;
//Вычисление матожидания среднеквадратичного изменения цены
double Edpp = (0.25 * plt.lj1 + plt.lj2);
double gv = -10000000;
int thmax = 1;
if (s == 0) thmax = 0;
double gvtemp = 0;
//Вычисление значений вероятности взятия лимитных ордеров в очереди заявок h(f)
//plt.ch - коэффициент в формуле для вероятности h(f)
double hresp = 0;
ClassMain.htfunc(plt.ch, new double[] { ft }, ref hresp, null);
double hresm = 0;
ClassMain.htfunc(plt.ch, new double[] { -ft }, ref hresm, null);
//Вычисление слагаемых ga и gb в выражении для оператора L, thmax - максимальное значение, которое принимает
// политика для лимитных ордеров - 1
for (int i = 0; i <= thmax; i++)
{
for (int k = 0; k <= thmax; k++)
{
gvtemp = (i * (plt.lMa) + (1 - i) * plt.lMa * hresp) * (plt.w[t+1,Math.Min(y + 1, (int)(2 * plt.Ymax)), f, s] - plt.w[t+1,y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * i) +
(k * (plt.lMb) + (1 - k) * plt.lMb * hresm) * (plt.w[t+1, Math.Max(y - 1, 0), f, s] - plt.w[t+1, y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if (gvtemp > gv)
{
gv = gvtemp;
plt.thmkb[t, y, f, s] = i; plt.thmka[t, y, f, s] = k;
}
}
}
//Вычисление значения оператора L (без умножения на матричную часть)
//plt.dt- шаг времени, plt.gamma - мера риска
double lv = plt.w[t+1, y, f, s] + plt.dt * yr * Edp + plt.dt * Ls - plt.dt * plt.gamma * yr * yr * Edpp + plt.dt * gv;
return lv;
}
Замечу, что вместо пассива для w[t,y,f,s] можно использовать всего два значения w0[y,f,s] и w1[y,f,s] - это значительно сэкономит память компьютера. где w[t+1,y,f,s] = w0[y,f,s]; w[t,y,f,s]=w1[y,f,s], в конце каждой итерации необходимо будет переобозначить все значения w0[y,f,s] = w1[y,f,s].
Итак, да не разозлится на меня автор, но я продолжаю разбор метода обратной индукции, и поиска оптимального решения. К сожалению, в указанном выше алгоритме также остаются существенные ошибки. Это определение элементов gv на краях, определение матрицы D2, а также неполное описание функции L. В настоящим момент производятся тестирования и поиск правильного решения. Как только оно будет получено, я подробно опишу все ошибки предложенного выше решения.
Ура! Получено устойчивое правильное решение, полностью соответствующее описанию в статье, и самое главное оно осуществленно согласно всем закладываемым логикам. Кроме того результат красивый. Настаиваю, что алгоритм автора (со всем уважением) не рабочий, несмотря на это выложенный код помог мне понять некоторые краеугольные камни в статье, за что отдельное спасибо. Рабочий алгоритм сформирован!!! К сожалению я не могу нормально в коментариях выложить его, также красиво как в статье. (см. выше - выложенный код получился нечитаемым). При условии что мне помогут правильно оформить код, я видоизменив оригинальный код программы ( сам я работаю в xe7 c++ ) выложу его в коментариях или ещё как-нибудь.
Ошибки содержались исключительно в алгоритме вычисления (неверно составлена матрица D2, неверно вычисляется значение gv на краях y, функция L должна быть полной, т.е. L[y,f,s], функция w - должна разделяться во времени о чём писал выше в коментариях, а также оператор L, и оператор MV должны вычисляться отдельно для всех значений y,f,s, кроме того мне понадобилось ввести дополнительно нормирующий коэффициент для функции w, который не влияет на результат, но не позволяет значению функции w сильно вырастать (при большом количестве значений времени вычисления и высоких значениях интенсивностей >2 переполняется стек переменной). Данный коэффициент не влияет на результат, но вычисления в свою очередь становится устойчивыми.
Кроме того, в своей программе код оптимизировал, значительно ускорив время вычисления. Библиотекой alglib не пользовался, так как в xe7 c++ она не применима, и алгоритмы обращения матрицы и умножения описывал вручную. Замечу (пусть и не по теме программы), что если библиотека alglib используется в режиме онлайн вычислений каждый тик или каждое обновление стакана, то лучше приобретите комерческую версию, так как в бесплатной алгоритмы библиотеки исключительно медленные.
я могу выложить ваш код отдельно в этой статье, если пришлете мне его по почте. К сожалению, так быстро не смогу его проверить, из-за загруженности, но вполне допускаю, что вы нашли правильные решения. Мой код был достаточно сырой, на практике я использовал только сильно упрощенные модификации, поэтому вам огромное спасибо за проделанную работу. Если вы уже дошли до проактического применения ( хотя бы до тестов), можно сделать отдельную статью на сайте по результатам.
а еще у меня возник вопрос. Судя по всему, вы пытаетесь вычислять политики в динамике, то есть перед выставлением ордеров пересчитываете весь алгоритм. Но нужно ли это делать? Может быть проще вычислить политики, например, за прошлый день, или несколько дней, а в текущем применять только карту этих политик в зависимости от входящих сигналов. Ведь если реакция на ваши сигналы устойчива, она не сильно изменяется в соседних торговых сессиях. Если же это не так, то сигналы неустойчивы и вообще вряд ли применимы в реальной торговле.
Нет, я не пересчитываю в динамике. Накапливаю данные за торговый период (1 день, либо пол дня) расчитываю политику и тестирую. Сегодня только первый день более менее адекватных тестов. Просто в ракурсе применения библиотеки allglib я уточнил, что в некомерческой версии авторы библиотеки используют крайне медленные , неоптимизированные алгоритмы, и в случае применения её в режиме мгновенных вычислений, лучше приобрести комерческую версию.
Сегодня переосмыслил полученные результаты, и убрал вообще все коэффициенты для функции владения, теперь алгоритм оригинальный и устойчивый. Оказывается к неустойчивости вычислений приводил большой шаг по времени ( в моём случае была 1 секунда). Поэтому в случае неусточивости вычислений следует просто уменьшить шаг по времени в 10 раз, если и в этом случае вычисления не устойчивы, то необходимо ещё раз уменьшить шаг по времени в 10 раз (однако в моём случае было достаточно шага 0.1 секунда). В оригинальной статье шаг брался 0.5 секунды, но там и интенсивности были в 10 и в 100 раз меньше. Решения получаются красивые. В частности неожиданной для меня политикой оказалась политика по дисбалансу (сигнал описываемый в статье выше) Видно сразу после получения политики, что сигнал имеет малую предсказательную способность, даже без теста, тем не менее он также достоин исследования.
В качестве вывода, хочу заметить, что основной упор рассматриваемого выше алгоритма это маркет-мейкинг. И в тестах необходимо делать упор именно на это направление, чем я и буду заниматься в самом ближайшем времени. Если честно я сомневаюсь что получу какие-либо значимые результаты особенно на индексе РТС, но ... надо проводить тесты и исследования.
Исправленный код отправил (пардон, хотел отправить - не получилось - не хватило лимита букв в смартлабе). Функция gv осталось прежней (это было целесообразно). После оптимизации программы оператор L принял прежний вид, то есть L[y,f]. Все остально откорректировал.
для отправки нужен электронный адрес.
мой адрес - uralpro@mail.ru
В матрице D2 неправильные значения при i==0 и i == F-1.
Должно быть так по идее:
if (i == 0)
{
D2[i, i + 1] = 2 1/ (dF * dF);
}
else if (i == F - 1)
{
D2[i, i - 1] =
21/ (dF * dF);}
else
{
D2[i, i - 1] = 1 / (dF * dF);
D2[i, i + 1] = 1 / (dF * dF);
}
D2[i, i] = -2 / (dF * dF);
Eskalibur, у вас так получилось? Интересно посмотреть какие еще изменения вы сделали в коде. Я переписал все расчеты на языке R, но результатами пока не очень доволен. Появляются какие-то непонятные области с где plt.thmka, plt.thmkb одновременно равны единице и активна политика лимитных оредеров. Да графике выходят кривые при спреде больше единицы. Интструмент Si, шаг времени 0.1, шаг сетки дисбаланса 0.1
Эх картинки не вставились
https://habrastorage.org/files/c5a/ca5/6e4/c5aca56e49b042688f154783c968fa2f.png
https://habrastorage.org/files/cb0/be2/8b1/cb0be28b1176421fb70ddaa629bfc0f1.png
добрый день. Все именно так:
if (i == 0)D2[i, i + 1] = 1/ (dF * dF);
else if (i == F - 1)D2[i, i - 1] = 1/ (dF * dF);
при других спредах могут быть кривыми если вы используете функцию w[y,f,s], выше в коментариях я указал что нужно разделять во времени - это и есть метод обратной индукции. Почему здесь нельзя так:
в момент времени t=T-1, при итерации s=0, в конце алгоритма уже получается новое значение w[y,f,s], при t=T-1 и s=1, функция w[y,f,s] вычисленная при s=0 опять учавствует в вычислениях при расчёте Ls. Таким образом она влияет на свой же результат внутри одной итерации по времени t=T-1, что приводит к накоплению во всех вычислениях ошибки. Поэтому нужно во всех вычислениях использовать значение функции w[t+1,y,f,s], а в конце итерации, где происходит сравнение L и M*L необходимо назначать w[t,y,f,s].
Касательно Си, у меня к Вам вопрос, - сколько значений спреда вы брали на си ? так как трех значений - на мой взгляд - там явно недостаточно. и второе, Jump модель изменения цены, на си опять же должна быть наверное другой, так как минимальный прыжок средней цены на minstep/2 (на si = 0.5 копеек) не случается - сишка прыгает минимум на minstep. Что вы делаете в этом случае ?
Количество значений спреда по Си у меня 10.
Jump модель такая же как в статье, и вроде все работает, ведь средняя цена - это просто среднее между лучшим бид и аском:
pricemid = (askprice0+bidprice0)/2
интенсивность прыжков pricemid/2 у вас чему равна на си?
Пардон, интенсивность прыжков minstep/2 у Вас чему равна ?
lambdaJ1 = 0.2374215
lambdaJ2 = 0.4438007
Дорабатывать ничего не пришлось. в алгоритме при расчёте прыжка на +минстеп/2 использовал функцию abs() которая ( WTF!???? ) возвращает только целое число. Поэтому у меня minstep/2 по сишке не обрабатывался.
Дьявол в деталях.
Кстати, интересный вопрос применения политик. Я на данный момент реализовал следующим образом:
1. Массивы политик расчитывыю за прошлый день. Таймфрэйм 1 секунда, шаг времени 0.1, спред 10, дисбаланс 10 с шагом 0.01, инвентори тоже 10, но максимальный размер рыночного лота ограничен 2 контрактами.
2. Далее по каждому новому тику расчитываю вектор t, y, f, s. Если открытых позиций нет (y=0), то ставлю время в 0.
3. Если есть открытые позиции, то время равно количеству милисекунд споследней сделки. Если есть неисполненые заявки:
- проверяю как далеко стоит завяка от текущих бид аск и снимаю, если ушли за пределы 10п
- пропускаю этот тик и иду на шаг 2 из расчета, что близкие к бид / аску заявки должны исполнится. В принципе, эту проверку можно будет в будущем убрать и постоянно забивать стакан новыми заявками.
3. Имея вектор t, y, f, s получаю политики из масивов и выставляю заявки по следующему алгоритму:
if(polmk==true)
{
if(thmka==0 && thmkb==0)
{
// Market Making policy
// Отправляем сигнал на покупку по лучшему биду
// Отправляем сигнал на продажу по лучшему аску
}
if(thmka==1 && thmkb==0)
{
// Pinging Ask Side policy
// Отправляем сигнал на продажу по лучшему аску - deltatick
}
if(thmka==0 && thmkb==1)
{
// Pinging Bid Side policy
// Отправляем сигнал на покупку по лучшему биду + deltatick
}
if(thmka==1 && thmkb==1)
{
// Pinging Bid & Ask Sides policy
// Отправляем сигнал на покупку по лучшему биду + deltatick
// Отправляем сигнал на продажу по лучшему аску - deltatick
}
}
if(polmk==false)
{
// Control policy
// Отпралвяем маркет сигнал на покупку (thtkq>0) или продажу (thtkq<0) с размером лота abs(thtkq)
}
Вопрос применения это просто актуальнейший вопрос. Честно говоря я пока не нашёл способа адекватно все применить и сам ищу ответы. правильно ли я понимаю, что в случае : if(thmka==1 && thmkb==0)
{
// Pinging Ask Side policy
// Отправляем сигнал на продажу по лучшему аску - deltatick
}
алгоритм выставляет только ордер на покупку, а в случае
if(thmka==0 && thmkb==1)
{
// Pinging Bid Side policy
// Отправляем сигнал на покупку по лучшему биду + deltatick
}
- только ордер на продажу ? Для меня пока моменты набора и сброса позиции остаются не ясными. Например , почему при pinging выставляются заявки только с одной из сторон. согласно политикам, насколько я понимаю (возможно и ошибочно), с одной стороны выставляется ордер на продажу(в случае // Pinging Ask Side policy) аск по бест аск-дельтатик, но политики не запрещают выставлять также ордер на покупку по бесббид.
в таком случае получается конечно получается не пойми что при и сбросе позы. можно внутри политики маркет-мейкинга напокупать и напродавать в убыток.
я пока нахожусь на стадии тестирования совместно с алгоритмом набора и сброса позиции.
1. Вначале торгов я выставляю два ордера на какое то расстояние от midprice. - на продажу и покупку соответственно. Если политика разрешает только в одну сторону , например покупка - то выставляю лимитный ордер с отступом (определённым заранее) от мидпрайс только в сторону покупки. В продажу не выставляю лимитный ордер если при изменении инвентори после взятия лимитника на продажу сгенерируется политика взятия по рынку 1 фьючерса. (то же самое с бидом).
2. Если лимитник взят, то ,опять же если разрешают политики, выставляю на следующую закупку лимитник ниже цены взятия с также с отступом , но отступ увеличиваю пропорционально набранной позиции в портфеле. Чем больше в портфеле, тем отступ на покупку от предыдущей покупки больше. (то же самое с набором шорта.)
3. Сброс позиции происходит обратным лимитником , который выставляется с определённым шагом от цены покупки (учитывается цена покупки каждого фьючерса). сначала продаётся фьючерс купленный по минимальной цене и т.д. Отступ для сброса позиции и набора позиции у меня разные и я подбираю их согласно результатам тестирования на истории.
4. При определённых политиках значениях инвентори и значениях индикатора происходит закрытие по рынку.
Но при таком алгоритме политики покупки по бесббиду или бестбиду+дельтатик не учитываются. Замечу , что на ри, пока не удалось вообще получить каких--то адекватных результатов. Вероятно применение какого-либо самостоятельного алгоритма маркет-мейкинга может быть ошибочным. Но честно говоря пока просвета в понимании как правильно это применить нет.
Попробую потестировать следующий варинт. Алгоритм (описанный мною выше) генерирует цены на взятие и закрытие. и если лучший бид и аск подходят к ним - выставлять заявки по этим ценам согласно политикам.
Столкнулся также со следующей проблемой при расширении спреда политика может диктовать условие взятия рыночным ордером. Выставляется лимитник. Он берётся. Далее спред сужается и политика по другому спреду говорит - закрыть позицию по рынку - получается убыточный трейд. Второй случае - спред сужается - заявка сразу же снимается. Т.о. растёт количество отменённых заявок. На ри, я тестировал алгоритм ( он в итоге оказался убыточным) у меня количество ордеров превышало 2500 за торговый день. Из них ополо 1800 отменённых, что просто требует оптимизации....
Короче думать. Идей нет пока адекватных. Если есть делитесь...
Кстати, ещё замечу что при расчёте политики по фьючам я беру гамму согласно примерному плечу =5. получается красивее и лучше чем если брать гамму =2 или гамму=1.
Также вопрос, если политики показывают при сильно положительном значении индикатора (дисбаланс объемов) вход лимитным ордером (политика маркет-мейкинга, и инвентори положительна) - мы можем лимитником - закрывать позицию, так как инвентори положительна и можем также лимитником набирать позицию. Понятно , что лимитники на закрытие инвентори будут иметь ЗНАЧИТЕЛЬНО большую вероятность исполнения. Тогда импульс просто не захватывается!!! и в моменте импульса происходит тупо сброс позиции. Что мы имеем в итоге - РЕБУС!
возможно у меня просто медленно транслируется стакан. Потому что у меня прыжки на си величиной minstep/2 пракически не происходят. Минимальный прыжок minstep.
Как у Вас результаты торгов на сишке ?
А как вы собираете данные и считаете рыночные коэффициенты? Я по каждому тику (сделке) пишу в общий масив собственно сам тик и параметры стакана в этот момент. Точность миллисекунда. Далее перед расчетом рыночных коэффициентов прореживаю масив по времени с точностью dt, где dt - это шаг времени в алгоритме. Таким образом скачки средней цены будут считаться не между наблюдениями, а за интервал dt.
Алгоритм пока не торговал. Отлавливаю ошибки, изучаю результаты. На данный момент получил такие графики:
<img src="https://habrastorage.org/files/06b/07e/fa0/06b07efa03c344708de651c2e09ebcb5.gif"/>
<img src="https://habrastorage.org/files/dba/632/8e8/dba6328e816248e791e0258051165db5.gif"/>
Все таки при больших значениях спреда, начинает вылазить непонятная область, где plt.thmka, plt.thmkb одновременно равны единице и активна политика лимитных оредеров. Обозвал ее PingingMarketMaking и буду дальше ковырять функцию расчета gv. Где-то там зарылась ошибка.
<img src="https://habrastorage.org/files/98d/e71/d21/98de71d2151545d4a44728e814e04a14.gif"/>
я вычисляю немного по-другому. мои алгоритмы вообще не работают со временем и синхронизацией. Все скачки midprice на minstep/2 и minstep записываются в массив. Для вычисления интенсивностей к каждому скачку присваивается значение времени затем количество скачков (количество элементов массива) делиться на время определяемое как разница между временем последнего и первого элемента. (все массивы кольцевые).
Изменение дисбаланса объема тоже собирается в массив. Каждое изменение записывается. Каждый апдейт стакана вычисляется дисбаланс, сравнивается с последним значением массива, и если он отличается от последнего значение то записывается в массив дисбаланса как новое следующее значение. Автоматически онлайн вычислются параметры процесса ОУ.
То есть данные из стакана записываются с каждым изменением стакана. Данные по тикам записываются с каждым новым тикам. Замечу что в алгоритме описанном в статье данные по тикам не используются, там только изменения стакана.
Касательно Вашего случая с большими значениями спреда. Думаю такая ситуация допустима. Когда большие значения спреда, то вполне возможно оптимальным решением выставлять и бид и аск ордера внутрь спреда (ведь единички означают именно это). так что не нахожу в этом ничего страшного. Значения политик которые представлены у Вас на мой взгляд очень адекватные, особенно в начальные моменты времени. у меня похожие на ри. Единственное на ри я использую всего 3 значения спреда и там политики plt.thmka, plt.thmkb при высоких спредах одновременно не равняются 1.
Но опять же я не использую политики близкие к моменту Т. Я использую только самую первую политику и в целях экономии памяти, и для целей тестирования это более чем достаточно.
Пришёл я к заключению, что при маркет-мейкинге важно применить какой-то алгоритм набора позиции. Так как ри очень трендовый, и очень волатильный, то если просто выставлять лимитники (при pol=1) по лучшему биду и аску (при plt.thmka=0 plt.thmkb =0) или по лучшей цене (plt.thmka=1 или plt.thmkb=1) алгоритм получается сливающий. А вот непосредственно измеряемый индикатор, будь то дисбаланс объёма или что-то подобное, это некая защита от большого слива при быстром тренде.
Замечу, что дисбаланс объемов на ри проявляет себя как очень очень контрендовый индикатор. То есть рост при падении, падение при росте. что в целом делает его не совсем адекватным для торговли фьючерсом РИ. Сегодня пока первый день тестирования. Так что каких-то значимых результатов не получил. Хотя определённый прогресс присутствует. Могу скинуть Вам на почту, в экселе политики для момента времени t=0, которые получил по данным накопленным за первую половину дня.
При наборе данных желательно попасть и в период роста рынка и в период падения, тогда не будет существенного смещения вероятностей, и соответственно политик.
Если вы не используете данные по сделкам, а только отслеживаете изменения стакана, то как считаете частоту прихода маркет ордеров на бид и аск (lambdaMa,lambdaMb)?
Да, совсем забыл, вы совершенно правы. Использую тики, для расчета вероятностей и интенсивностей по бидам и аскам.
r0man, проверьте следующий момент. Я не пришёл в этих исследованиях к однозначным выводам... в функции gv на краях (когда y=Ymax и y=-Ymax) при вычислениях возможно нужно убирать одно из слагаемых. Иначе получается , что реально на этом шаге инвентори не увеличивается и не уменьшается (для y=Ymax и y=-Ymax соответственно), а плюсовое значение взятия половины спреда к функции владения прибавляется. Я вначале использовал gv, на краях по одному слагаемому, но меня что-то не устроило. Сейчас при тестировании других сигналов, я с исправленной функцией gv получаю адекватные политики. Возможно у Вас сформируется более чёткое мнение на этот счет, так как вы работаете с сишкой.
Не, этот подход неправильный! все - подтверждено железно! больше к этому вопросу не возвращаюсь! gv - расчитана изначально верно.
Расчет gv у меня такой же. Поставил алгоритм на тестирование. Пока все политики очень четко отрабатывают.
Я а сишку буду дорабатывать позже. Буду незначительно изменять алгоритм, у меня минимальынй прыжок си =минстеп. Соответственно марковская модель будет чуть измененя.
Но сначала ри обкатаю, счас глубоко в тестах. Обкатка и доработка программы дорогое удовольствие )).
у меня честно говоря, для сишки, очень странные политики получились ... не могу понять в чем дело.... Например при спреде =0, в инвентори вообще не должно быть позиций ....
похоже надо завести отдельную тему для обсуждения алгоритма исследуемого алгоритма...
Давайте установим взаимопонимание. Может быть мы по-разному представляем себе как должны работать политики.
Итак, я понял, что политики имеют следующее значение:
если политика =1, то работа ведётся только лимитниками. далее смотрятся thmka и thmkb.
- если thmka=1 , то на продажу выставляется лимитник по bestask-deltatic, если =0, то лимитник только на bestask.
- если thmkb=1, то на покупку лимитник по bestbid+deltatic, если thmkb=0, то лимитник только на bestbid.
если политика = 0, то выставляются только ордера по рынку.
Вообще, согласно статье при политике ММ (1) должны выставляться лимитные ордера и на бид и на аск одновременно. При tmka=0, tmkb=0 (а также при непонятной зоне где tmka=1, tmkb=1) я так и делаю. Если только единице равен только один из показателей, то я выставляю только один лимитник bestbid+deltatic или bestask-deltatic. Возможно, это не совсем верно, но я объясняю это тем, что зоны pinging ask side (pinging bid side) возникают у меня только при открытой позиции лонг (шорт).
А вообще, нужно бы взять все коэффициенты из статьи и прогнать через алгоритм, чтобы провреить получаются такие же графики политик или нет. У меня до сих пор сомнения в правильности расчетов, может быть упустил какую-то мелочь. Например зоны Momentum Control у меня вообще не появляются.
Еще я проверяю немного другой расчет дисбаланса. Беру логарифм разности СУММЫ объемов бидов / асков по глубине стакана. Глубина 5.
Дисбаланс я исследовал точно также как и Вы. логарифм глубины =5. Согласно правильности ваших расчётов я напишу коментарий ниже! Вы оцените. Надеюсь автор сайта тоже оценит, ибо это невероятно чудо - то что я осознал с алгоритмом обратной индукции!
Касательно дисбаланса - моё заключение следующее. Согласно моим наблюдениям в фортсе дисбаланс это контртрендовый сигнал. В статье дисбаланс был представлен как трендовый. Наверное лучше считать для нас дисбалан как log(ask)-log(bid) - тогда сигнал будет трендовый! И вот почему - на западе движущей силой являются трейдеры, фонды и т.п. На нашем рынке -специалист. Он сдвигает рынок согласно своему инвентори. То есть у нас ситуация со стаканом зеркальная. На западе стакан наполняют участники - у нас те кто наполняет стакан это минимум участников и специалист. Основные участники рынка бьют в стакан. Об этом же говорил Майтрейд. что он долго не мог понять почему у нас на рынке и на западе ситуация зеркальная. Он пришёл к заключению ( я с ним согласен) что основной контрагент участников на фортсе это маркет-мейкер (или мистический кукл, Лези Манухар =) ). Специалист накапливает портфель, потом убирает свою ликвидность, рынок сдвигается для нового равновесия и там уже разгружает с прибылью. Есть диссертация на эту тему в сети, как два три крупных участника - как правило это иностранные контрагенты - огромными деньгами выкачивают ликвидность из фортса. Пока рынок в диапазоне они забирают акции раздают бабки трейдерам, банкам и т.п.. На рынке возникает избыток денег и нехватка акций. Рынок сдвигается за пару дней в новое равновесное состояние - он поднимается в цене. На этом уровне происходит разгрузка. Все это на Фортсе происходит из за черезвычайно малой ликвидности. Вот моё мнение на этот счет.
Честно говоря адаптация этого алгоритма на наш рынок достаточно не простая задача. Но на мой взгляд этот подход имеет огромный потенциал. В этом ракурсе я не понимаю, как автор сайта (да прибудет с ним сила =) ) проработал его, упростил и использует. Гений!!!
Открыл какой-то суперэффективный сигнал видимо...
Адаптация алгоритма - всегда непростая задача. Но, по-моему, вы уже достаточно далеко продвинулись. Тут главное не сдаваться, я некоторые алгоритмы по полгода мучил, без каких-то видимых результатов. Это на самом деле довольно однообразная и скучная работа, но правильный результат может все компенсировать. Сигнал, да, другой несколько применяю, чем в статье, но близко к тому. Тут ключевое слово - market impact 🙂
Интересно, но непонятно... Что с этой информацией делать не знаю. Но использовать хочется 🙂 !
Как-то интуитивно я чувствую, что Вы подтолкнули меня к некоторым очень важным вещам... Дисбаланс объёмов тут может играть очень важную роль...
Итак, друзья. Представленный в статье алгоритм расшифрован. Это озарение случилось со мной в 16:15 25.06.2015. Я получил много даров от автора сайта, и от пользователя r0man в качестве его мнения и спешу отблагодарить. Большое Вам спасибо за участие в беседе и помощи в понимании. В обмене мнением и вашим коментариям как бесполезным так и полезным. Надеюсь что мы будем сотрудничать и в будущем, и сможем быть полезными друг для друга!
Ошибка закралась в политики при вычислении функции gv. у меня тоже в политиках появлялись иногда артефакты которые были не существенными, но портили красоту картины и сеяли сомнения! Все артефакты появлялись на краях инвентори!
Ниже код для расчёта gv на краях инвентори, при y=-Ymax и y=Ymax который убирает некрасивые артефакты:
if(y<2*ycount && y>0){
for (i = 0; i <= thmax; i++) {
for (k = 0; k <= thmax; k++){
gvtemp =(i*lmdask+(1-i)*lmdask*hask)*(w[t+1][y+1][f][s]-w[t+1][y][f][s]+(s+1)*minstep/2-minstep*i)+
(k*lmdbid+(1-k)*lmdbid*hbid)*(w[t+1][y-1][f][s]-w[t+1][y][f][s]+(s+1)*minstep/2-minstep*k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if(i>0 || k>0){
if(gvtemp > gv){
gv = gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
}
else if(i==0 && k==0){
gv=gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
};
};
}
else if(y==2*ycount){
for (i = 0; i <= thmax; i++) {
for (k = 0; k <= thmax; k++){
gvtemp =(i*lmdask+(1-i)*lmdask*hask)*(w[t+1][y][f][s]- w[t+1][y-1][f][s]+(s+1)*minstep/2-minstep*i)+
(k*lmdbid+(1-k)*lmdbid*hbid)*(w[t+1][y-1][f][s]-w[t+1][y][f][s]+(s+1)*minstep/2-minstep*k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if(i>0 || k>0){
if(gvtemp > gv){
gv = gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
}
else if(i==0 && k==0){
gv=gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
};
};
}
else if(y==0){
for (i = 0; i <= thmax; i++) {
for (k = 0; k <= thmax; k++){
gvtemp =(i*lmdask+(1-i)*lmdask*hask)*(w[t+1][y+1][f][s]- w[t+1][y][f][s]+(s+1)*minstep/2-minstep*i)+
(k*lmdbid+(1-k)*lmdbid*hbid)*(w[t+1][y][f][s]-w[t+1][y+1][f][s]+(s+1)*minstep/2-minstep*k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if(i>0 || k>0){
if(gvtemp > gv){
gv = gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
}
else if(i==0 && k==0){
gv=gvtemp;
thmkb[y][f][s]=i;
thmka[y][f][s]=k;
};
};
};
};
Важные блоки я выделил жирным цветом. Коментировать не буду!
Итак далее! к вопросу почему нет маркет ордеров или как я описал выше (у меня при нулевом спреде не было в инвентори позиций вообще)! Для этого существует параметр гамма!!!! Если не существует ордеров по рынку - повышайте гамму до 5, до 10-ти . Если же наоборот - нет маркет ордеров, и инвентори пуста - нужно уменьшать гамму. Мне пришлось уменьшить гамму на си до 0.1 - тогда все получилось!
r0man, давайте искать прибыльный алгоритм с применением политик. Ясно что посылать заявки согласно статье сразу на лучший бид и аск не работает.
Вообще для этих целей, может быть сделать некую закрытую область сайта, или ещё как !?. Это уже инсайд. Проделана гора работы. Потеряны какие-то деньги при отработке... Или же чат для обсуждения, который не публикуется ...
Сделал чат для общения - страница ChatRoom в верхнем меню. Чтобы начать приватный чат, нужно нажать на имя пользователя. с которым хотите общаться. Для общения пользователи должны быть залогинены
gamma - говорит об влиянии шума в торговле. То есть если визуально stock очень трендовый, то гамма нужно уменьшать. 1 и меньше. Если график цены похож на флэт с выбросами то гамму нужно увеличивать. Чем уже флэт, тем больше гамма.
Это справедливо в случае если индикатор в основе алгоритма трендовый. Контртрендовые индикаторы не проверял.
Здравствуйте! А ChatRoom больше не работает? Есть вообще те, кто еще занимается данным алгоритмом?
Не совсем понятно как в принципе может возникать политика Momentum описанная во второй части, так как согласно данному коду, количество контрактов не может быть больше максимально допустимого на данном шаге: