Итак, по результатам голосования в лидерах оказалась публикация Alvaro Cartea и Sebastian Jaimungal "Algorithmic Trading of Co-integrated Assets". Я тоже считаю эту работу очень интересной, так как она фактически расширяет понятие парного трейдинга до торговли произвольным количеством активов, с учетом их коинтеграционного взаимоотношения. Это сильно повышает устойчивость результирующего портфеля, в отличие от парного трейдинга, в связи с его диверсификацией.
Представляю здесь перевод этой статьи, которую я несколько сократил, убрав длинные математические выкладки и оставив только наиболее важные и окончательные формулировки. Думаю, это значительно облегчит понимание, без утраты основного смысла публикации.
Вступление
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
В данной работе мы создадим оптимальную стратегию, в которой агент открывает позиции в n коинтегрированных активах. Цель стратегии - получение прибыли от структурной зависимости в динамике их цен . Мы предполагаем, что активы коинтегрированы и создадим алгоритмическую торговую стратегию, где инвестор максимизирует ожидаемую функцию владения ( то есть вложенные и наличные средства). Мы выведем отдельную закрытую формулу для оптимальной (динамической) инвестиционной стратегии и покажем, что она учитывает коинтеграционный фактор. Далее, мы используем данные торгов с биржи Nasdaq для калибровки модели и проведем симуляцию, чтобы продемонстрировать, насколько стратегия производительна, в случае, когда инвестор открывает позиции в трех активах : Google, Facebook и Amazon.
Мы предполагаем, что дрифт в приращениях цен активов состоит из компонента, присущего только данному активу, и общего компонента для всех используемых активов. Общий компонент, который мы называем краткосрочной альфа, представляет собой процесс возврата к среднему с нулевым средним, являющийся естественным источником прибыли в торговой стратегии - он определяет прибыль от краткосрочных инвестиционных возможностей для коллекции активов.
Коинтегрированные логарифмы цен с краткосрочной альфа
Предположим, что дрифт в приращениях цен активов состоит из особого и общего компонентов. Особый компонент есть результат факторов, влияющих только на каждый отдельный актив, и общий компонент - результат индустриального или секторального набора факторов, которые влияют на всю коллекцию используемых активов. Таким образом, у нас есть коллекция активов, чей вектор цен обозначим 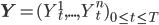 , который удовлетворяет системе дифференциальных уравнений:
, который удовлетворяет системе дифференциальных уравнений:
\begin{equation}\frac{dY_t^k}{Y_t^k}=(\nu_k+\delta_k\alpha_t)dt+\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
где особый компонент 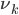 является константой, и общий компонент :
является константой, и общий компонент :
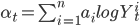 ,
,
где 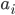 - константы, и
- константы, и 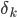 - специальная константа , которая показывает, как общий компонент влияет на каждый актив.
- специальная константа , которая показывает, как общий компонент влияет на каждый актив.
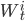 - стандартные Броуновские движения, независящие друг от друга, собранные в вектор
- стандартные Броуновские движения, независящие друг от друга, собранные в вектор 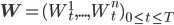 , и
, и 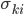 - неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
- неотрицательные константы. Мгновенную ковариацию между активами i и j можно определить как:
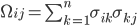 .
.
Далее, обозначим  матрицу, чьими элементами являются
матрицу, чьими элементами являются 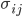 , представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы
, представляющую собой разложение Холецкого мгновенной дисперсионно-ковариационной матрицы 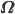 , таким образом
, таким образом 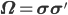 , где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что
, где ' обозначает оператор транспонирования. Предположим, что нет дополнительных степеней свободы, так что  является обратимой.
является обратимой.
Покажем, что  ведет себя как фактор коинтеграции. Когда
ведет себя как фактор коинтеграции. Когда 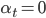 все активы являются геометрическими броуновскими движениями с дрифтом
все активы являются геометрическими броуновскими движениями с дрифтом 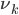 . В общем случае, на рынках акций,
. В общем случае, на рынках акций,  будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
будет ненулевой и отклонения от ее долгосрочного или предсказуемого уровня быстро нивелируются. Такое поведение этого компонента мы назовем краткосрочной альфа, и она представляет собой отклонения от ожидаемого приращения активов.
Докажем, что  является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
является коинтеграционным фактором, продемонстрировав, что это, несомненно, процесс возврата к среднему. Во-первых отметим, что логарифмы цен удовлетворяют дифференциальному уравнению:
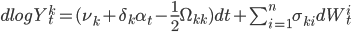 ,
,
которое мы используем для вычисления дифференциала  :
:
\begin{equation}d\alpha_t=\sum_{k=1}^n a_k(\nu_k+\delta_k\alpha_t-\frac{1}{2}\Omega_{kk})dt+\sum_{k=1}^n a_k\sum_{i=1}^n\sigma_{ki}dW_t^i\end{equation}
Таким образом, мы можем записать компонент краткосрочной альфы как процесс возврата к среднему:
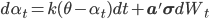 , где
, где
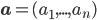
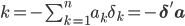 ,
,
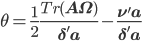 .
.
Здесь, оператор Tr() обозначает след матрицы, и А=diag(a) - диагональная матрица, чья диагональ состоит из а. Для уверенности, что модель действительно описывает процесс возврата к среднему, мы предположим, что 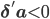 - и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
- и это мы увидим в результатах калибровки модели на реальных данных с биржи Nasdaq.
Рассматривая динамику (2), мы можем видеть, что  возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую
возвращается к среднему с частотой, которая зависит от различной степени воздействия, какую  оказывает на каждый актив (через
оказывает на каждый актив (через 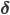 ), а также от силы вклада логарифма цены актива в саму
), а также от силы вклада логарифма цены актива в саму  (через а). Уровень возврата к среднему
(через а). Уровень возврата к среднему 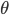 зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
зависит от отношения волатильности к воздействию каждого компонента на общий дрифт активов и на дрифт каждого актива.
Альтернативное представление модели можно вывести, поместив выражение для  непосредственно в дифференциальное уравнение для
непосредственно в дифференциальное уравнение для 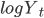 . В этом случае, мы получаем:
. В этом случае, мы получаем:
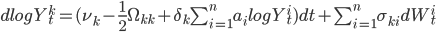 ,
,
и если мы обозначим 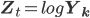 , где логарифм применен к каждому компоненту, то
, где логарифм применен к каждому компоненту, то
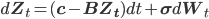 ,
,
где 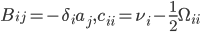 .
.
В этом представлении мы видим, что логарифм цены представляет собой векторно-авторегрессивную модель 1 порядка (VAR(1)). Отметим здесь, что B - вырожденная матрица. которая имеет одно положительное собственное значение, соответственно единственному фактору коинтеграции, который мы заложили в модель.
В следующей части мы найдем оптимальное динамическое уравнение распределения активов для нашего портфеля в закрытой форме, а затем продемонстрируем, как использовать выведенные формулы на практике, на примере портфеля из трех акций.

 (9 голосов, средний: 4,56 из 5)
(9 голосов, средний: 4,56 из 5)


Настолько же наукообразно как и бесполезно. Ранее (в видео) было еще более наукообразно показано, что при количестве активов >2, описание их корреляции через парную корреляцию является приближенной и в общем случае надо учитывать корреляции (ковариации) болше чем пары.
Короче: что дает эта модель для практической реализации? Разве не есть самое точное, что можем получить - это тупо взять и промоделировать на истории? А если нужны статистические оценки будущего, то можно и забутстрапить (хотя к адекватности этой процедуры тоже есть вопросы).
Здесь как раз и учитывается коинтеграция множества активов. И сделано довольно изящно и просто, далее это будет показано. Используется авторегрессивная модель VAR, то есть простая регрессия - вы ее в любом случае должны использовать для определения коэффициентов. А затем по вычисленным значениям рассчитывается функция оптимальной доли каждого актива по одной формуле. Что может быть проще? По-моему это и называется - тупо взять и промоделировать на истории ( разве что потом применить оптимальную функцию).
Модель учитывает только парную ковариацию, а этого мало, если n>2
Главное, зачем она нужна для практики? Разве не проще подобрать несколько (>2) инструментов из имеющихся моделируя на истории м сделать выводы о будущей статистике просто глядя на историческую эквити?
И еще, чем больше инструментов, тем хуже соотношение возможной прибыли к комиссии.
Модель учитывает совместную коинтеграцию активов, иначе зачем было городить огород с матрицами?
Матрица она двумерная, годится для случай n=2. При n=3 для полноценной модели ковариаций требуется куб и т.д. Но по большиму счету это все бесполезно на практике.
Матрица она двумерная, годится для случай n=2. При n=3 для полноценной модели ковариаций требуется куб и т.д. Но по большиму счету это все бесполезно на практике.
По-моему вы чего-то не понимаете. Для записи ковариаций n активов нужна обычная двумерная матрица n x n
Матрица только парные корреляции покажет, но не все скажет про корреляции >2 инструментов.
https://www.lektorium.tv/lecture/26007
uralpro, специально для тебя нашел то самое место в большой лекции https://www.youtube.com/watch?v=HOrnHWucJnk&feature=youtu.be&t=1280
Но там еще много интересного
День добрый. Спасибо за потраченное время на перевод и обработку статьи.
Но, как обычно при изучении научных трудов, присутствует некоторый дискомфорт. Поэтому, если возможно, не могли бы вы сделать небольшое пояснение или уточнение.
Ознакомившись бегло с оригиналом в т.ч., не уловил предварительные условия или критерии отбора инструментов -кандадитов на включение в расчет.
Не совсем понятны критерии отбора кандидатов: каков предварительный тест на зависимость?
Или предполагается, что в форме прогона заодно и станет ясна применимость модели, о которой говорит Роман, то есть ставим инструмент, и если есть зависимость, то модель выплывет?
Ну тогда, сильно извиняюсь, есть варианты попроще для восприятия, а, может быть и понадежнее, а также с просто реализуемыми онлайн-алгоритмами - время обновления модели можно вписать в микросекунды. Хотя, конечно, и с этой моделью можно повозиться.
Как известно, ключевая задача - это обнаружение признаков-кандидатов на построение модели зависимости, а уже далее можно делать и последующие настройки.
Не могли бы вы уточнить, каким образом делается поиск признаков, и в чем на ваш взгляд, особенность достижения трудящихся Alvaro Cartea и Sebastian Jaimungal?
Об отборе кандидатов в статье не упоминается. Предполагается, что кандидаты уже известны. Для отбора можно использовать стандартные техники - например, тесты на коинтеграцию и стационарность спреда, описанные во множестве статей и книг, например Vidyamurthy - Pairs Trading. Данная статья совсем не об этом, а о том, как выделить коинтеграционный компонет в случае использования нескольких активов. И я совсем не считаю, что ключевой задачей является отбор кандидатов. В любой, самой коинтегрированной паре спред когда-нибудь разойдется. Поэтому самое главное - техника торговли, позволяющая динамически контролировать позиции. А в этой статье именно это и описано - можно динамически вычислять ошибки регрессии на любом количестве активов и в реальном масштабе времени определять доли вложения в каждый актив.
Предлагаю немного улыбнуться.
Вопрос к классикам покера: Нужна ли математика в покере?
Склански (Профессор, чемпион мира и т.д., а также автор трудов по теории игры и Покеру в частности, по объему приближающихся к творениям Д.Кнута "Искусство программирования для ЭВМ") - желательна.
Какова доля математики (по сути оптимальный размер ставки согласно обстоятельствам - местоположение в турнире, стадия, позиция и т.д....) - около 15%, т.к. основным является навык чтения оппонента и умение получить оплату.
---
Однозначно выбор признаков (факторов) в широком смысле является самой сложной задачей.
---
Спасибо за ответ.
Спасибо за перевод!
Пара опечаток: в левой части уравнения для Z(t) пропущен дифференциал; в определении элементов матрицы B потерян знак.
Спасибо за замечания. Исправил
Подскажите что изучить на русском языке что бы понять эту статью, почитал в интернете про корреляцию, коинтеграцию, но понимания сильно не прибавилось. Нашел на сайте Булашева это оно? Посоветуйте с чего начать чтоб не отвернула
На русском языке очень мало написано по этим темам, все в основном англоязычное. Книга Булашева - очень полезная, но там даны только основы. Постараюсь на этом сайте еще написать статьи про коинтеграцию