QuantAlgos

В прошлой части мы рассмотрели теоретическую модель, лежащую в основе вычисления вероятности присутствия на рынке информированных трейдеров PIN. Продолжим с эмпирической реализации этой модели.

Для уменьшения пространства параметров модели, обычно предполагают, что частоты прихода ордеров на продажу 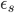$\epsilon_s$ и на покупку 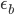$\epsilon_b$ равны. В день "хорошей новости" вероятность наблюдения последовательности сделок купли и продажи соответствует:

$\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^B}{B!}\exp(\epsilon T)\frac{(\epsilon T)^S}{S!}$, где B и S - число сделок купли и продажи соответственно.

Для дней  "плохой новости":

$\exp(\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^S}{S!}$.

И для дней с отсутствием новостей вероятность равна:

$\exp(\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(\epsilon T)\frac{(\epsilon T)^S}{S!}$.

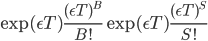Предполагая, что торговая активность независима от одного дня к другому в течении T дней, вероятность торговой активности принимает форму:

$L[\{B,S\}|\theta]=(1-\alpha)\exp(-\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-\epsilon T)\frac{(\epsilon T)^S}{S!}+\alpha\delta\exp(-\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^S}{S!}+\alpha(1-\delta)\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^B}{B!}\exp(-\epsilon T)\frac{(\epsilon T)^S}{S!}$

с пространством параметров 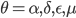$\theta=\alpha,\delta,\epsilon,\mu$. За h независимых дней вероятность наблюдения 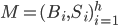$M=(B_i,S_i)_{i=1}^h$ равна произведению дневных вероятностей:

$L[M|\theta]=\prod_{h=1}^h L(\theta|B_i,S_i)$.

Для сходимости при численной максимизации преобразуем функцию вероятности следующим образом:

$L[M|\theta]=\sum_{i=1}^T[-2\epsilon+M_t\ln(x)+(B_t+S_t)\ln(\mu+\epsilon)]+\sum_{i=1}^T\ln[\alpha(1-\alpha)\exp(-\mu)x^{S_t-M_t}+\alpha\delta\exp(-\mu)x^{B_t-M_t}+(1-\alpha)x^{B_t+S_t-M_t}]$

где $M_t=\min(B_t,S_t)+\max(B_t,S_t)/2, x_t=\epsilon/(\mu+\epsilon)$.

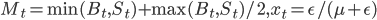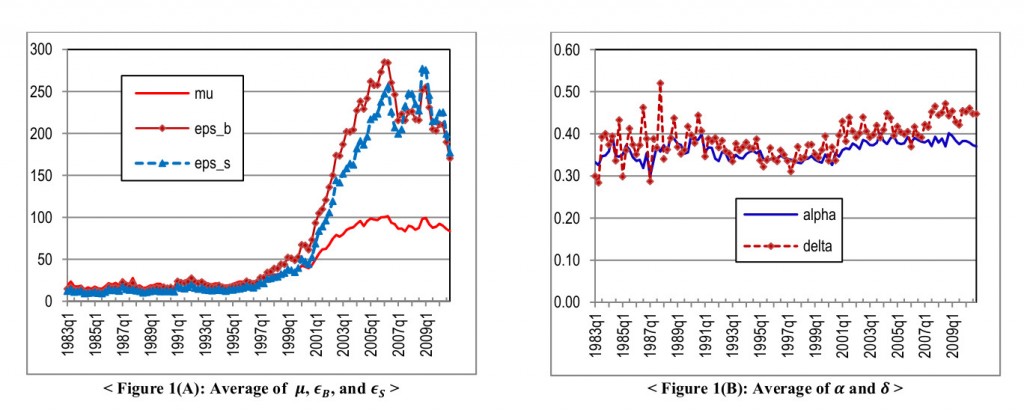
Найти параметры 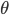$\theta$ можно методом численной максимизации вышеприведенной вероятности (в заглавии поста приведены графики полученных параметров для акций NYSE с 1983 по 2009 год). После этого мы сможем найти индикатор информированной торговли PIN, который равен безусловной вероятности того, что информированные участники покупают или продают актив в каждый момент времени:

$PIN_t=\frac{\alpha\mu}{\alpha\mu+2\epsilon}$.

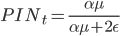Когда значение PIN велико, неинформированные трейдеры сталкиваются с высоким риском того, что их контрагент в сделках лучше информирован. В своих алгоритмах необходимо учитывать этот индикатор и предпринимать  соответствующие действия при его высоком значении, например, снимать ордера, противоположные текущему направлению движения цены.

Пакет PIN языка R содержит функцию для вычисления логарифма вероятности торговой активности. На вход она принимает значения параметров - 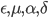$\epsilon,\mu,\alpha,\delta$ - и временную последовательность дневных данных с числом сделок купли и продажи, помещенных в матрицу размерностью n х w, где n - число торговых дней. Первая колонка матрицы содержит число сделок купли, вторая - число сделок продажи.

В следующей части мы рассмотрим практический пример с использованием языка R, где  применим численную максимизацию упомянутой выше функции и получим значения параметров, а затем, соответственно, вычислим PIN.