QuantAlgos

Перевод статьи из блога Эрни Чана.

Все знают, что значение волатильности зависит от частоты измерений: стандартное отклонение 5-минутных приращений цены отличается от стандартного отклонения дневных приращений. Если z - логарифм цены, то волатильность, взятая на интервале 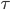$\tau$, рассчитывается следующим образом:

$volatility(\tau)=\sqrt(Var(z(t)-z(t-\tau)))$

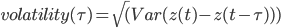
где под Var понимается дисперсия на множестве интервалов. Если цены действительно представляют собой процесс геометрического случайного блуждания, то:

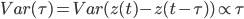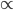$Var(\tau)=Var(z(t)-z(t-\tau)) \propto \tau$ ($\propto$ - символ пропорциональности)

и волатильность просто изменяется пропорционально квадратному корню из интервала выборки. Поэтому, если мы берем дневные приращения, то должны умножить дневную волатильность на корень из 252 для получения годовой волатильности.

Трейдеры также знают, что цены в реальности не следуют геометрическому случайному блужданию. Если цена следует процессу возврата к среднему, мы увидим, что она не уходит от своего начального значения так быстро, как бы это было при случайном блуждании. А если цена следует тренду, то она будет двигаться быстрее. В общем, мы можем записать:

$Var(\tau) \propto \tau^{2H}$

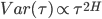
где Н называется "экспонентой Херста", и она равна 0.5 для истинного геометрического случайного блуждания, но меньше 0.5 для процесса возврата к среднему, и больше 0.5 для тренда.

Если мы приведем к году волатильность цен, следующих процессу возврата к среднему, то получим значение годовой волатильности меньше, чем для геометрического случайного блуждания, даже если оба процесса имеют одинаковую волатильность, измеренную, скажем на 5-минутных интервалах. Обратное верно для цен, следующих тренду. Например, если мы сделаем это для валютной пары AUDCAD, очевидно следующей процессу возврата к среднему, то получим Н=0,43.

Все вышесказанное хорошо известно. Но интересно то, что экспонента Херста может быть разной на отличающихся временных интервалах, и эта разница иногда говорит о смене режима с процесса возврата к среднему к импульсному режиму, или наоборот. Для иллюстрации, построим график волатильности (или точнее дисперсии), как функции от 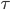$\tau$. Часто такой график называют временной структурой (реализованной) волатильности.

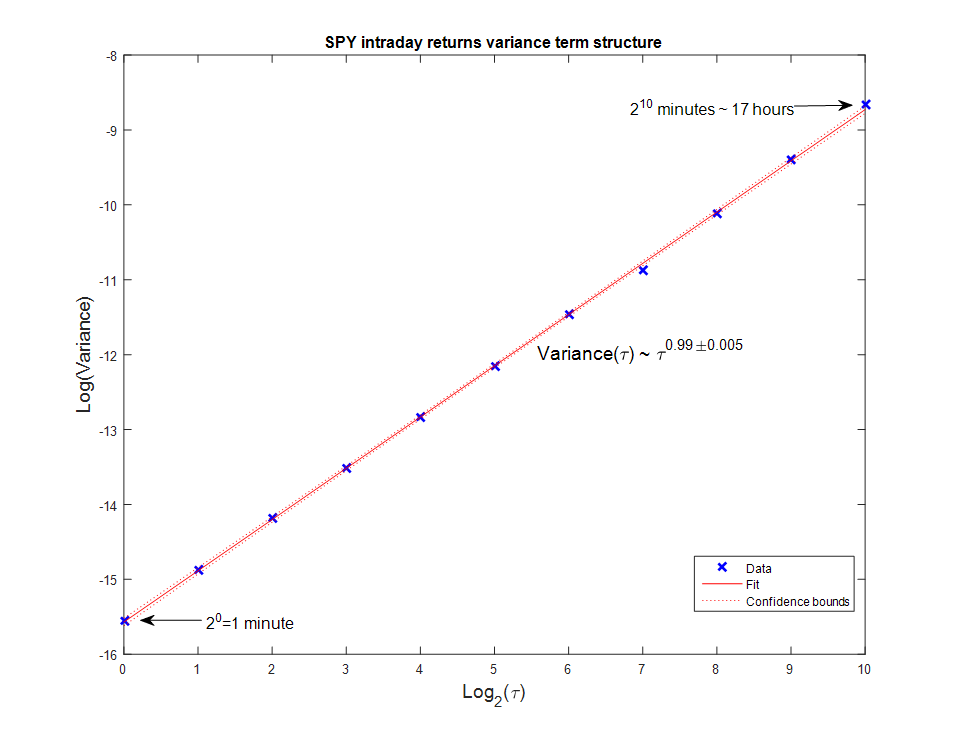
Начнем с обычного SPY. Вычислим внутридневные приращения, используя средние цены от первой минуты до 2^10 минуты (примерно 17 часов) и построим график 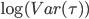$\log(Var(\tau))$ относительно 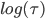$log(\tau)$. Аппрокимация прямой линией на графике в заглавии получилось отличной. Наклон линии, деленный пополам, является значением экспоненты Херста, которая получается равной 0.494+/-0.003, что говорит об очень слабой степени возврата к среднему.

Но если мы сделаем то же самое для дневных приращений SPY, для интервала от 1 дня до 256 , то получим Н=0.469+/-0.007, что говорит о значительной степени возврата к среднему.

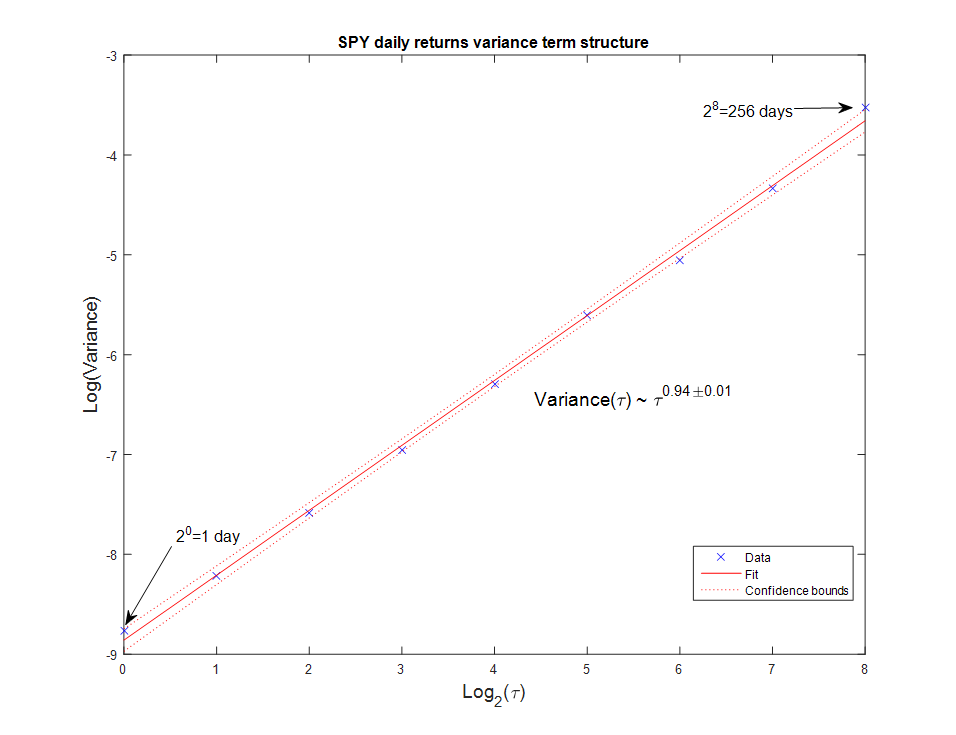Вывод: стратегии возврата к среднему на SPY толжны работать лучше на дневных интервалах, чем на внутридневных.

Мы можем сделать то же самое для инструмента USO (ETF на фьючерсы сырой нефти WTI). Внутри дня H=0.515+/-0.001, показывает значительную трендовую составляющую. Дневной Н=0.056+/-0.02 демонстрирует еще большую долю тренда. Таким образом, импульсные стратегии для фьючерсов на сырую нефть будут работать на любых разумных временных интервалах.

Давайте попробуем протестировать GLD, ETF на золото. Внутридневной Н=0.505+/-0.002, что говорит о слабом тренде. Но дневной H=0.469+/-0.007: значительный перевес возврата к среднему! Импульсные стратегии на золоте могут работать внутри дня, но стратегии возврата к среднему будут работать лучше на множестве дней. Где происходит этот переход? Мы можем исследовать временную структуру детально:

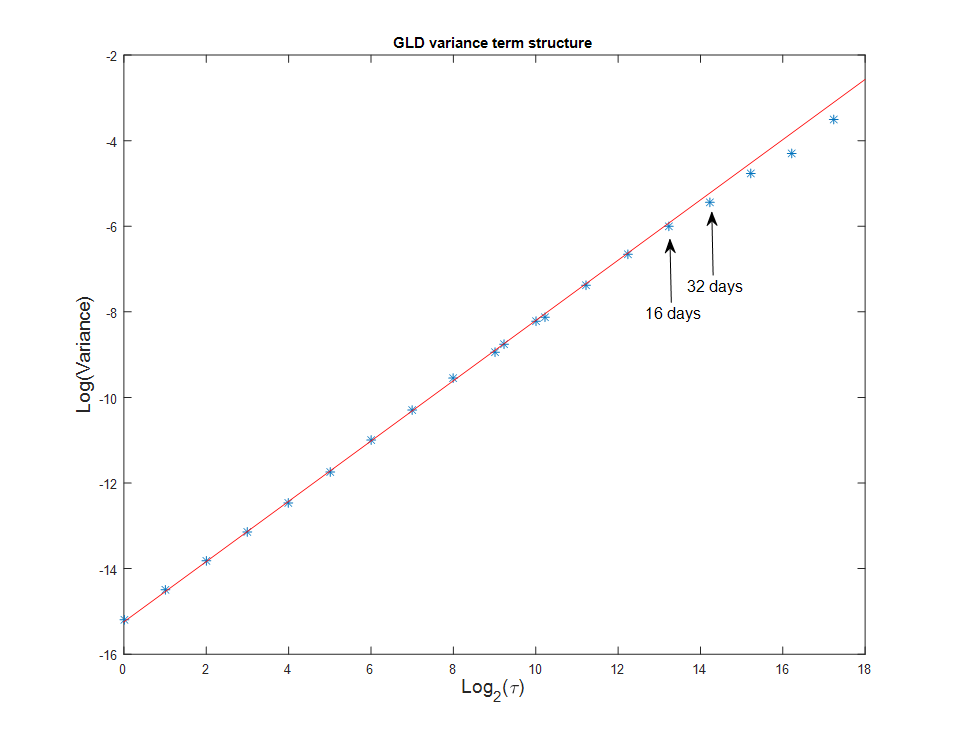Можно заметить, что в районе 16-32 дня волатильность отходит от прямой линии, экстраполирующей внутридневные частоты. Здесь и происходит скачок от импульсных стратегий к стратегиям возврата к среднему.

Одно замечание: когда мы вычисляем дисперсию приращений за период, захватывающий два торговых дня и строим зависимость от 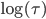$\log(\tau)$, должен ли интервал 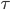$\tau$ включать часы, когда рынок закрыт? Ответ должен быть да, но не совсем. В процессе построения графиков выше, где дневные дисперсии вначале попадают на ту же прямую линию, что и внутридневные, мы должны считать один торговый день эквивалентным 10 торговым часам. Не 6,5 часам (как для рынка акций США) и не 24 часам. Точное число торговых часов, конечно, разное для разных инструментов.