Небольшая статья по парному трейдингу на американском рынке акций от студентов Колумбийского университета Peng Huang и Tianxiang Wang с практическими примерами (оригинал).
Разница между применямой нами и обычной практикой парного трейдинга в том, что мы используем метод максимального правдоподобия для конструирования оптимального портфеля статического парного трейдинга, который наиболее соответствует процессу Орнштейна-Уленбека, и строго определяем его параметры. Таким образом, мы убеждаемся, что наши портфели следуют процессу возврата среднего перед тем как начинать торговлю. Затем мы генерируем контртрендовые торговые сигналы, используя параметры модели. Также мы оптимизируем пороги и величину периодов in-sample и out-of-sample. Для примера, акции Crown Castle International Corp. (CCI) и HCP, Inc. (HCP) при таком подходе показывают коэффициент Шарпа 2.326 на периоде in-sample и 2.425 на периоде out-of-sample. Акции Crown Castle International Corp. (CCI) и Realty Income Corporation (O), торгуемые по нашей методике, демонстрируют коэфициент Шарпа 2.405 и 2.903 соответственно на выборках in-sample и out-of-sample.
1.Введение
Стратегии возврата к среднему широко используются на практике. Тем не менее, не всегда есть уверенность, что функция стоимости портфеля соответствует процессу возврата к среднему, перед применением стратегии.
Мы исследуем широкий спектр акций для нахождения пары, подходящей под процесс Орнштейна-Уленбека. Затем мы торгуем портфель таких пар в соответствии с нашими торговыми правилами. Так же, как и в других mean reversion стратегиях, мы продаем, когда величина портфеля аномально высока, и покупаем, когда она экстремально низкая. Кроме того, мы оптимизируем входные/выходные сигналы. Для этого мы тестируем серию пороговых значений. Затем вычисляем коэффициент Шарпа, годовую прибыль, максимальную просадку, частоту сделок, торговый диапазон, прибыль на сделку для различных порогов. Выбираем наилуший порог по тесту на out-of-sample. Далее, выбираем различные индустриальные и экономические циклы с целью найти подходящий период in-sample для каждой пары. Как правило, мы тестируем 4 разных периода in-sample , но оставляем период out-of sample постоянным. В итоге, мы нашли 9 пар, которые показывают высокую прибыльность как в тренировочных, так и в проверочном периодах. Все эти пары демонстрируют коэффициент Шарпа более 1.9 на тестах in-sample и out-of-sample. Далее, мы выяснили, что когда спредовый гэп между входным и выходным сигналом узкий, то частота сделок будет высокой. Если же выходной сигнал около 0, то время удержания позиции увеличивается. Такие результаты легко понять, представив, что при узком гэпе торговый сигнал достигает порогов чаще. А когда сигнал закрытия близок к нулю, то вероятность исполнения меньше. В данной работе мы обобщим статистические результаты для девяти пар и покажем их детально для двух пар.
2.Методология
Наше применение парного трейдинга имеет включает две стадии - тренировочный и проверочный периоды. Во-первых, мы формируем пары, используя метод максимального правдоподобия на тренировочной выборке. Затем мы тестируем торговую стратегию с различными порогами и находим лучшие входной/выходной сигнал. Во-вторых, в тесте на проверочной выборке исследуем выбранные пары с 23.12.2014 года по 10.11.2015 года (200 дней). Мы пробовали периоды различной длины (880 дней, 628 дней, 376 дней и 124 дня) для нахождения наиболее предсказательного для нашей проверочной выборки.
2.1. Формирование пар
Выберем пять секторов из 156 индустриальных подразделений, перечисленных в классификационном стандарте Global Industry Classification Standard (GICS), а именно банки, программное обеспечение и интернет-службы, финансовые службы, недвижимость и здравоохранение. Затем возьмем любые две акции из каждого сектора. Отметим, что все наши акции входят в индекс S&P500.
Наш портфель состоит из длинной позиции из  контрактов актива
контрактов актива 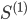 и короткой позиции из
и короткой позиции из 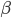 контрактов другого актива
контрактов другого актива 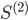 :
:
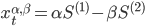
Для нахождения лучшей 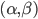 стратегии, мы ссылаемся на метод, предложенный в Leung, T. and Li, X. (2016). Optimal Mean Reversion Trading: Mathematical Analysis and Practical Applications. World Scientific Publishing Co. Используем метод максимального правдоподобия для приведения наблюдаемой функции стоимости портфеля к процессу Орнштейна-Уленбека и определим парметры модели. Затем найдем значения
стратегии, мы ссылаемся на метод, предложенный в Leung, T. and Li, X. (2016). Optimal Mean Reversion Trading: Mathematical Analysis and Practical Applications. World Scientific Publishing Co. Используем метод максимального правдоподобия для приведения наблюдаемой функции стоимости портфеля к процессу Орнштейна-Уленбека и определим парметры модели. Затем найдем значения 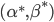 по наибольшему среднему логарифма функции правдоподобия.
по наибольшему среднему логарифма функции правдоподобия.
Если подробней, представим, что мы инвестируем А долларов в актив 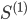 , так что
, так что 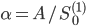 . Соответственно, мы продаем
. Соответственно, мы продаем 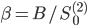 контрактов актива
контрактов актива 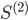 , где В/А=0.001,0.002,...,1. Для примера, установим А=1. Таким образом, для каждой пары сделаем
, где В/А=0.001,0.002,...,1. Для примера, установим А=1. Таким образом, для каждой пары сделаем  постоянной, в то время как B будет меняться от 0.001 до 1. Применим оценку по методу максимального правдоподобия для нахождения параметров процесса Орнштейна-Уленбека, которому соответствует наша функция стоимости портфеля
постоянной, в то время как B будет меняться от 0.001 до 1. Применим оценку по методу максимального правдоподобия для нахождения параметров процесса Орнштейна-Уленбека, которому соответствует наша функция стоимости портфеля 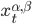 . Далее мы определим B , который соответствует наибольшему значению логарифму функции правдоподобия.
. Далее мы определим B , который соответствует наибольшему значению логарифму функции правдоподобия.
2.2 Генерация торговых сигналов
Будем торговать только в том случае, когда обнаружим аномальное отклонение. Установим окно в 60 рабочих дней. Каждый торговый день используем данные внутри этого окна для вычисления параметров процесса Орнштейна-Уленбека.
Процесс Орнштейна-Уленбека:
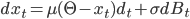
Равновесная дисперсия:
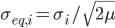
Соответственно, определим безразмерную переменную (торговый сигнал) для пары i :
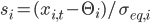
После применения метода максимального правдоподобия, можно вычислить оценки всех параметров модели. Таким образом, мы рассчитаем торговый сигнал 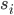 для каждого дня.
для каждого дня.
Наши правила возврата к среднему:
-
открываем длинную позицию, если
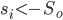
-
открываем короткую позицию,если
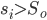
-
закрываем короткую позицию,если
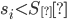
-
закрываем длинную позицию, если
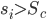
Протестируем 20 порогов 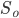 и 20 порогов
и 20 порогов 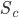 . В общем, у нас есть 400 пар порогов.
. В общем, у нас есть 400 пар порогов.
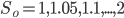
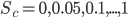
В следующей части выберем оптимальные пороги, рассчитаем параметры прибыльности полученных стратегий и приведем практические примеры.



Ссылка на оригинал битая немного, легко исправить, но может кто-то не допетрит. Отличная статья, спасибо за перевод, даже жалко, что буду читать оригинал все равно.
Спасибо за замечание, исправил