Вариант стратегии, использующей ассиметрию статистического распределения доходности, рассмотрен в блоге blog.johnorford.com.
Напомню, приращение цены какого-либо актива равна разнице между его ценой в конце расчетного периода и ценой начала периода:
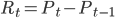 .
.
Если подсчитать общее количество каждого значения приращения за промежуток времени, намного большего периода его расчета, а затем построить гистограмму, где на оси абсцисс будет значение приращения, а на оси ординат - число таких значений за рассматриваемый период времени, то получим плотность статистического распределения приращений цен актива:
 Асимметрией назывется отношение третьего момента к среднеквадратичному отклонению, а простыми словами - если на гистограмме хвост распределения справа от нуля больше, то говорим о положительной асимметрии приращения, если больше хвост слева - то об отрицательной. Положительная асимметрия говорит о том, что за рассматриваемый период было больше плюсовых приращений цены, отрицательная - было больше минусовых приращений.
Асимметрией назывется отношение третьего момента к среднеквадратичному отклонению, а простыми словами - если на гистограмме хвост распределения справа от нуля больше, то говорим о положительной асимметрии приращения, если больше хвост слева - то об отрицательной. Положительная асимметрия говорит о том, что за рассматриваемый период было больше плюсовых приращений цены, отрицательная - было больше минусовых приращений.
Как можно использовать асимметрию в качестве индикатора покупки/продажи? Представим, что асимметрия не изменяется слишком быстро. Тогда покупаем, если асимметрия, например, за прошлую неделю была положительной, продаем в обратном случае. Автор проверил такую стратегию на 65-летней выборке данных индекса S&P и получил коэффициент Шарпа около 0,1. Значит есть порядка 20% шансов, что такая стратегия не будет прибыльной в дальнейшем. Не очень хороший результат.
Попробуем улучшить производительность стратегии. Создадим индикатор, который будет зависеть не от уровня асимметрии, а от ее изменения от месяца к месяцу, предположив, что эта разница будет лучше отображать настроение на рынках.
Определим точные формулы для нашего индикатора. Когда ассиметрия приращения цен S&P возрастает то мы вычисляем его следующим образом, при этом покупая актив пропорционально значению :
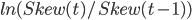 ,
,
когда асимметрия падает, удваиваем значение индикатора, сокращая актив также пропорционально (но не менее 0):
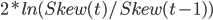 .
.
(как вычисляется непосредственно ассиметрия плотности распределения можно найти здесь).
В среднем за весь рассматриваемый период мы владели примерно 2% индекса и на 98% были в кэше. Без удвоения в случае сокращения асимметрии в среднем бы у нас было 0,03% индекса, сликом малое значение. Удвоение выбрано достаточно произвольно, но позволяет быть в позиции больше времени, что увеличивает производительность стратегии.
В результате, коэффициент Шарпа стратегии превысил коэффициент Шарпа индекса S&P500 за последние 25 лет, и теперь шанс, что стратегия не будет прибыльной в дальнейшем уменьшился до 1%. Кумулятивный коэффициент Шарпа для индекса и стратегии показан на графике в заглавии поста. Этот показатель для нашего алгоритма оставался очень стабильным как минимум 20 лет. В 2008 году заметно большое падение коэффициента, после чего он быстро восстановился для нашей стратегии, гораздо быстрее, чем для индекса.
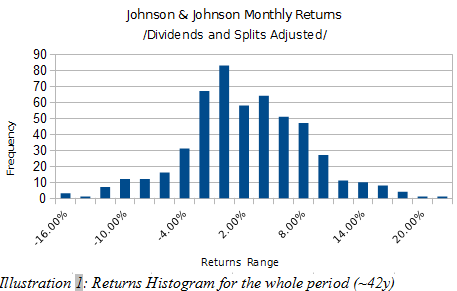
В итоге, сам наш алгоритм демонстрирует позитивную асимметрию. На гистограмме ниже показана плотность распределения месячных приращений цен для S&P за последние 25 лет. Асимметрия здесь равна примерно -1. Левый хвост длинее правого.
Другая картина складывается для нашей стратегии. Потери сильно ограничены в размере по сравнению с прибылью. Значение ассиметрии между 3 и 4:
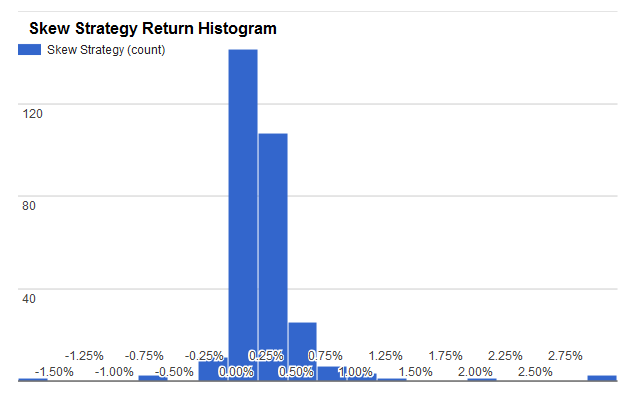 При всем при этом коэффициент бета между S&P500 и нашим алгоритмом всего около 0,02. Это говорит о том, что наша стратегия слабо повторяет движения индекса, следовательно мало зависит от долгосрочных трендов в нем.
При всем при этом коэффициент бета между S&P500 и нашим алгоритмом всего около 0,02. Это говорит о том, что наша стратегия слабо повторяет движения индекса, следовательно мало зависит от долгосрочных трендов в нем.
Казалось бы, не так много разумного можно извлечь из такого обычного индикатора, как асимметрия. Однако показатели рассмотренной стратегии позволяют сделать вывод, что даже из простых индикаторов можно создать достаточно производительный алгоритм.

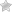 (3 голосов, средний: 4,00 из 5)
(3 голосов, средний: 4,00 из 5)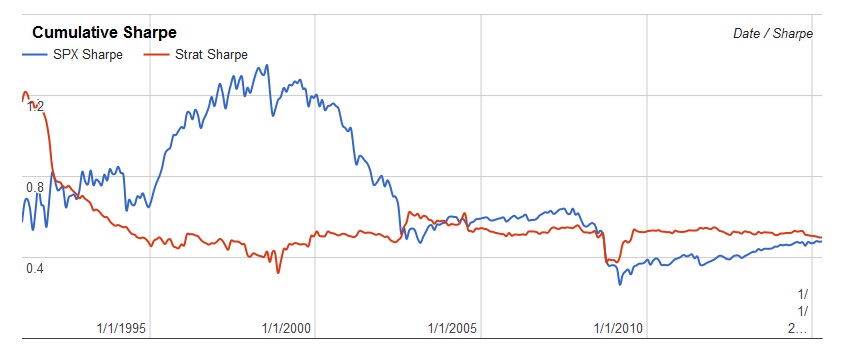


Доходность актива не равна разнице цен. Доходность либо считается как
R(t) = { R(t) - R(t-1) } / R(t-1) , либо
R(t) = log( R(t) / R(t-1) )
Да, вы правы. Здесь речь идет о приращении цены, я это исправил
Что то я вообще не понял по этой стратегии. Те считаем раз в месяц ассиметрию и если выросла то покупаем уменьшилась продаем?
Или мы считаем раз в месяц по более мелким таймфрэймам?
как описано в в тексте: "покупаем, если асимметрия, например, за прошлую неделю была положительной, продаем в обратном случае". Приращения, например, можно посчитать за 1 час, а распределение построить недельное.
Те по сути на растущем рынке выкупаем просадки а на падающем продаем отскоки?
фактически так